题目内容
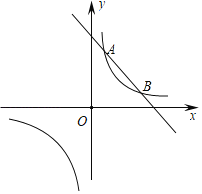
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线一定过原点②方程ax2+bx+c=0(a≠0)的解为x=0或x=4,③a﹣b+c<0;④当0<x<4时,ax2﹣bx+c<0;⑤当x<2时,y随x增大而增大,其中结论正确的个数( )
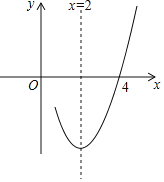
A. 1B. 2C. 3D. 4
【答案】C
【解析】
由抛物线的对称轴结合抛物线与x轴的一个交点坐标,可求出另一交点坐标,结进而结合图形分析得出答案.
①∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),
∴抛物线与x轴的另一交点坐标为(0,0),结论①正确;
②∵抛物线与x轴的交点坐标为:(0,0),(4,0),
∴方程ax2+bx+c=0(a≠0)的解为x=0或x=4,正确;
③∵当x=﹣1和x=5时,y值相同,且均为正,
∴a﹣b+c>0,结论③错误;
④当0<x<4时,ax2﹣bx+c<0,结论④正确;
⑤观察函数图象可知:当x<2时,y随x增大而减小,结论⑤错误.
综上所述,正确的结论有:①②④.
故选:C.

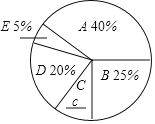
【题目】“全民阅读”活动,是中央宣传部、中央文明办和新闻出版总署贯彻落实关于建设学习型社会要求的一项重要举措.读书必须要讲究方法,只有按照一定的方法去阅读,才能取得事半功倍的效果.常用的阅读方法有:A.圈点批注法;B.摘记法;C.反思法:D.撰写读后感法;E.其他方法.某县某中学张老师为了解本校学生使用不同阅读方法读书的情况,随机抽取部分本校中学生进行了调查,通过数据的收集、整理绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
中学生阅读方法情况统计表
阅读方法 | 频数 | |
A | 圈点批注法 | a |
B | 摘记法 | 20 |
C | 反思法 | b |
D | 撰写读后感法 | 16 |
E | 其他方法 | 4 |
(1)请你补全图表中的a,b,c数据:a= ,b= ,c= ;
(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有 人;
(3)小明从以上抽样调查所得结果估计全县6000名中学生中有1200人采用“撰写读后感法”读书,你同意小明的观点吗?请说明你的理由.
(4)该校决定从本次抽取的“其他方法”4名学生(记为甲,乙,丙,丁)中,随机选择2名成为学校阅读宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
【题目】某校创建“环保示范学校”,为了解全校学生参加环保类社团的意愿,在全校随机抽取了50名学生进行问卷调查.问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团,也可以不选),对选择了社团的学生的问卷情况进行了统计,如下表:
社团名称 | A 酵素制作社团 | B 回收材料小制作社团 | C 垃圾分类社团 | D 环保义工社团 | E 绿植养护社团 |
人数 | 10 | 15 | 5 | 10 | 5 |
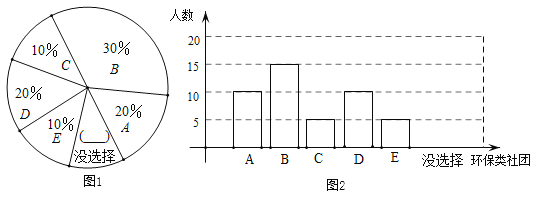
(1)根据以上信息填空:这5个数的中位数是______;扇形图中没选择的百分比为______;
(2)①补全条形统计图;②若该校有1400名学生,根据调查统计情况,请估计全校有多少学生愿意参加环保义工社团;
(3)若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加,请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率.