题目内容
【题目】如图，已知直线
与双曲线
交于A、B两点，点B坐标为(-4,-2)，C为双曲线
上一点，且在第一象限内，若△AOC面积为6，则点C坐标为（ ）
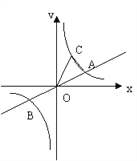
A. （4,2） B. （2,3） C. （3,4） D. （2,4）
【答案】D
【解析】
∵点B(4,2)在双曲线
上， 
，∴k=8.
∵点A，点B关于原点对称，所以A(4,2)，
如图,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,设点C的坐标为
，
若S△AOC=S△COF+S梯形ACFE-S△AOE
.∵△AOC的面积为6， 
，整理得,a2+6a16=0，
解得a1=2,a2=8(舍去)，∴点C的坐标为(2,4).
作AE⊥x于点E, CF⊥x于点F.
S△AOC=S△AOE+S梯形ACFES△COF
.
∵△AOC的面积为6， 
，即
.
解之得：a=8或a=2(舍去)
∴点C的坐标为(8,1).
故答案为：(2,4)或(8,1).
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
