题目内容
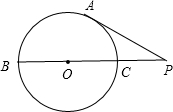 如图:已知点P是⊙O 外一点,PA是⊙O的切线,切点为点A,连接PO并延长交⊙O于点C、B.
如图:已知点P是⊙O 外一点,PA是⊙O的切线,切点为点A,连接PO并延长交⊙O于点C、B.(1)如果PB=3PC,求∠P的度数;
(2)如果PB=m•PC,∠P=45°,求m的值.
分析:(1)连接OA,则OA⊥PA.根据已知条件易得OP=2OA,从而求得∠P的度数;
(2)如果∠P=45°,那么△AOP是等腰直角三角形.设半径为x,分别表示PB、PC,得方程求解.
(2)如果∠P=45°,那么△AOP是等腰直角三角形.设半径为x,分别表示PB、PC,得方程求解.
解答: 解:(1)连接OA.(1分)
解:(1)连接OA.(1分)
∵PA是⊙O的切线,
∴OA⊥PA,即△OAP是直角三角形.(1分)
∵PB=PC+CO+BO,
PB=3PC,BO=CO,
∴PC=CO.(1分)
又PO=PC+CO,
∴PO=2OC.
∵OA=OC,
∴PO=2OA.(1分)
∴∠P=30°.(1分)
(2)由(1)得△OAP是直角三角形.
∵∠P=45°,
∴∠AOP=45°.
∴OA=PA.(1分)
设OA=x,则OB=OC=PA=x.
根据勾股定理得:PO=
x.
∴PB=PO+BO=
x+x,(1分)
PC=PO-OC=
x-x.(1分)
∵PB=m•PC,
∴
x+x=m•(
x-x),(1分)
∴m=3+2
.(1分)
 解:(1)连接OA.(1分)
解:(1)连接OA.(1分)∵PA是⊙O的切线,
∴OA⊥PA,即△OAP是直角三角形.(1分)
∵PB=PC+CO+BO,
PB=3PC,BO=CO,
∴PC=CO.(1分)
又PO=PC+CO,
∴PO=2OC.
∵OA=OC,
∴PO=2OA.(1分)
∴∠P=30°.(1分)
(2)由(1)得△OAP是直角三角形.
∵∠P=45°,
∴∠AOP=45°.
∴OA=PA.(1分)
设OA=x,则OB=OC=PA=x.
根据勾股定理得:PO=
| 2 |
∴PB=PO+BO=
| 2 |
PC=PO-OC=
| 2 |
∵PB=m•PC,
∴
| 2 |
| 2 |
∴m=3+2
| 2 |
点评:此题考查切线的性质及等腰直角三角形的性质,涉及二次根式的计算,综合性较强.

练习册系列答案
相关题目
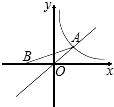 如图,已知点A是函数y=x与y=
如图,已知点A是函数y=x与y=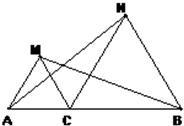 20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.
20、如图,已知点C是AB上一点,△ACM、△CBN都是等边三角形.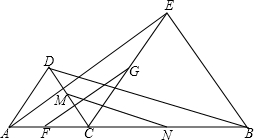 M、N分别是线段AC、CE、CD、CB的中点,
M、N分别是线段AC、CE、CD、CB的中点,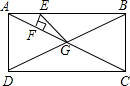 如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG=
如图,已知点E是矩形ABCD的边AB上一点,且EF⊥AC,EG⊥BD,AB=4cm,AD=3cm,则EF+EG= 如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.
如图,已知点C是线段AD的中点,AC=15cm,BC=22cm,分别求线段AD和BD的长度.