题目内容
 如图,E是在正方形ABCD的延长线上一点,且CE=AC.则∠E=________.
如图,E是在正方形ABCD的延长线上一点,且CE=AC.则∠E=________.
22.5°
分析:AC为正方形ABCD的对角线,AC即∠BAD和∠BCD的角平分线,因为E在BC的延长线上,即B、C、E三点一线,且AC=CE,所以∠E=∠CAE,且∠E+∠CAE=∠ACB=45°.
解答:正方形的各角平分线,对角线,重合,
∴AC即∠ACD的角平分线,
即∠ACB=45°,
∵∠ACB为△ACE的外角,
∴∠CAE+∠E=∠ACB,
∵AC=CE
∴∠CAE=∠E.
∴∠E=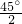 =22.5°,
=22.5°,
故答案为22.5°.
点评:本题考查了正方形对角线即角平分线的性质,考查了等腰三角形底角相等的性质,本题中根据∠CAE=∠E和∠CAE+∠E=∠ACB求∠E是解题的关键.
分析:AC为正方形ABCD的对角线,AC即∠BAD和∠BCD的角平分线,因为E在BC的延长线上,即B、C、E三点一线,且AC=CE,所以∠E=∠CAE,且∠E+∠CAE=∠ACB=45°.
解答:正方形的各角平分线,对角线,重合,
∴AC即∠ACD的角平分线,
即∠ACB=45°,
∵∠ACB为△ACE的外角,
∴∠CAE+∠E=∠ACB,
∵AC=CE
∴∠CAE=∠E.
∴∠E=
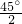 =22.5°,
=22.5°,故答案为22.5°.
点评:本题考查了正方形对角线即角平分线的性质,考查了等腰三角形底角相等的性质,本题中根据∠CAE=∠E和∠CAE+∠E=∠ACB求∠E是解题的关键.

练习册系列答案
相关题目
 如图,E是在正方形ABCD的延长线上一点,且CE=AC.则∠E=
如图,E是在正方形ABCD的延长线上一点,且CE=AC.则∠E= (2012•邵阳)如图所示,在正方形网格中(网格中每个小正方形的边长均为1),将△OAB绕点O按逆时针方向旋转,得到△OCD,则∠AOC的度数是
(2012•邵阳)如图所示,在正方形网格中(网格中每个小正方形的边长均为1),将△OAB绕点O按逆时针方向旋转,得到△OCD,则∠AOC的度数是
