题目内容
(15分)已知方程2(m+1)x2+4mx+3m=2,根据下列条件之一求m的值.
(1)方程有两个相等的实数根;
(2)方程有两个相反的实数根;
(3)方程的一个根为0.
(1)m1=-2,m2=1;(2)m=0;(3)
【解析】
思路点拨:利用一元二次方程的判别式以及根与系数的关系来解答本题.
试题分析:△=16m2-8(m+1)(3m-2)=-8m2-8m+16,
(1)方程有两个相等的实数根,
∴△=0,即-8m2-8m+16=0,求得m1=-2,m2=1;
(2)因为方程有两个相等的实数根,
所以两根之和为0且△≥0,则- =0,求得m=0;
=0,求得m=0;
(3)∵方程有一根为0,∴3m-2=0得
考点:判别式;根与系数的关系

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 B.
B. C.
C. D.
D.
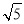 D.8
D.8
 与
与
 与
与
 与
与
 与
与