��Ŀ����
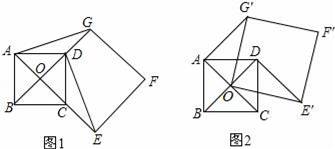
��ͼ����֪������y=ax2+bx��3��x�ύ��A��B���㣬��y�ύ��C�㣬����A��B��C�����Բ��Բ��M��1��m��ǡ���ڴ������ߵĶԳ����ϣ���M�İ뾶Ϊ
 �����M��y�ύ��D�������ߵĶ���ΪE��
�����M��y�ύ��D�������ߵĶ���ΪE��
��1����m��ֵ�������ߵĽ���ʽ��
��2�����DBC=������CBE=�£���sin�������£���ֵ��
��3��̽�����������Ƿ���ڵ�P��ʹ����P��A��CΪ��������������BCE���ƣ������ڣ���ָ����P��λ�ã���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�


�����㡿���κ����ۺ��⣮
��ר�⡿ѹ���⣻�����ͣ�
����������1������������ͼ��ɵõ�C�����꣬����Բ�����ʿɵõ�B�����꣬���ݶԳ��᷽�����B�����꼴����ú����Ľ���ʽ��
��2���������ߵĽ���ʽ����õ�A��E��B��C��D�����꣬�ж�Rt��BOD��Rt��BCE���á�CBE=��OBD=�£����sin�������£�=sin����DBC����OBD��=sin��OBC=
 ��
��
��3����ȻRt��COA��Rt��BCE����ʱ��P1��0��0����
��A��AP2��AC��y��������P2����Rt��CAP2��Rt��BCE����P2��0��
 ����
����
��C��CP3��AC��x��������P3����Rt��P3CA��Rt��BCE����P3��9��0����
�����������ϴ���������P1��0��0����P2��0��
 ����P3��9��0����ʹ����P��A��CΪ��������������BCE���ƣ�
����P3��9��0����ʹ����P��A��CΪ��������������BCE���ƣ�
����𡿽⣺��1���������֪C��0����3������
 =1��
=1��
�������ߵĽ���ʽΪy=ax2��2ax��3��a��0����
��M��MN��y����N������CM����MN=1��CM=
 ��
��
��CN=2������m=��1��
ͬ�������B��3��0����
��a��32��2a��3��3=0����a=1��
�������ߵĽ���ʽΪy=x2��2x��3��
��2���ɣ�1����A����1��0����E��1����4����B��3��0����C��0����3����
��M��AB��CD�ľ�����ȣ�OB=OC��
��OA=OD��
���D��������0��1����
����Rt��BCO��BC=
 =3
=3
 ��
��
��
 ��
��
�ڡ�BCE�У���BC2+CE2=��32+32��+[��1��0��2+����4+3��2]=20=��3��1��2+��0+4��2=BE2���BCE��Rt��

 ��
��
��
 ��
��
��
 ��
��
��Rt��BOD��Rt��BCE���á�CBE=��OBD=�£�
���sin�������£�=sin����DBC����OBD��=sin��OBC=
 ��
��
��3����ȻRt��COA��Rt��BCE����ʱ��P1��0��0����
��A��AP2��AC��y��������P2��
��Rt��CAP2��Rt��BCE����P2��0��
 ����
����
��C��CP3��AC��x��������P3����Rt��P3CA��Rt��BCE����P3��9��0����
�����������ϴ���������P1��0��0����P2��0��
 ����P3��9��0����
����P3��9��0����
ʹ����P��A��CΪ��������������BCE���ƣ�


�����������⿼���˶��κ�����Բ��֪ʶ���ۺ�Ӧ�ã�Ҫע�����ͼ�Σ�Ӧ�����������ε��������ж���Ҫע�����ν��˼���Ӧ�ã�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
 �£�1+
�£�1+
 ��������x=
��������x=
 ��
��


 xƽ�ƺ�O���������Ϊ6�����Bƽ�Ƶľ���Ϊ��������
xƽ�ƺ�O���������Ϊ6�����Bƽ�Ƶľ���Ϊ��������



 +����3.14��0��
+����3.14��0��


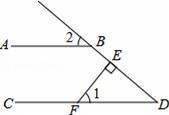
 ����һ���㹻���ֱ�����ǰ��ֱ�Ƕ�����ڵ�A
����һ���㹻���ֱ�����ǰ��ֱ�Ƕ�����ڵ�A ����CD���ڵ�F����CB�ӳ��߽��ڵ�E���ı���AECF�������(�� )
����CD���ڵ�F����CB�ӳ��߽��ڵ�E���ı���AECF�������(�� )