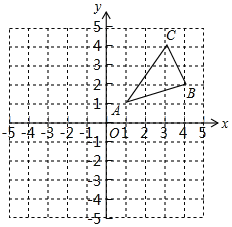Question

【题目】（1）解方程：；

（2）如图，在平面直角坐标系中，的三个顶点的坐标分别为、、．

①将向左平移5个单位得到，写出三顶点的坐标；

②将绕原点逆时针旋转后得到，请你画出；

③与重合部分的面积为 ．（直接写出）

Answer 1

【答案】（1），；（2）①，，；②见解析；③

【解析】

（1）利用因式分解法解一元二次方程即可；

（2）①将向左平移5个单位得到，根据点的平移规律：左减右加、上加下减，即可得出结论；

②将绕原点逆时针旋转后得到即可；

③设A1C1与A2C2交于点D，找出与重合部分△A2C1D，然后证出△A1A2C1是直角三角形，并求出其面积，然后证出⊥，根据三线合一和三角形中线的性质即可求出结论．

（1）解：，

∴，

∴，

（2）①将向左平移5个单位得到，如图所示，即为所求

∵、、

∴，，

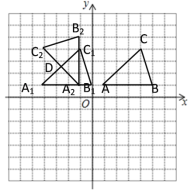
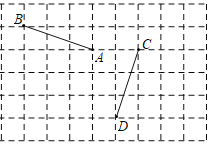
②将绕原点逆时针旋转后得到，如图所示，即为所求；

③设A1C1与A2C2交于点D，

由平面直角坐标系可知：A2的坐标为（-1,1），与重合部分为△A2C1D

∴A2C1 =A1A2=3，且∠A1A2 C1=90°

∴△A1A2C1是直角三角形，

∴S△A1A2C1=A2C1·A1A2=

∵是由AC平移得到，是由AC绕原点逆时针旋转90°得到

∴∥AC，⊥AC

∴⊥

∴点D为A1C1的中点

∴S△A2C1D=S△A1A2C1=