题目内容
已知圆O的弦AB=8，相应的弦心距OC=3，那么圆O的半径长等于分析：连接圆心和弦的一端，在构造的直角三角形中，通过解直角三角形即可求出⊙O的半径．
解答：
解：如图，连接OA；
由于OC⊥AB，所以AC=BC=4；
在Rt△OAC中，OC=3，AC=4，由勾股定理得：
OA=
=5；
即⊙O的半径为5．
解：如图，连接OA；由于OC⊥AB，所以AC=BC=4；
在Rt△OAC中，OC=3，AC=4，由勾股定理得：
OA=
| AC2+OC2 |
即⊙O的半径为5．
点评：此题主要考查的是垂径定理和解直角三角形的综合应用．
练习册系列答案
相关题目
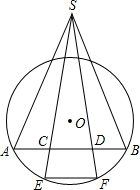如图，已知圆O的弦AB被点C、D三等分，又E、F是弧AB的三等分点，连接EC、FD交于S，连接SA、SB，求证：∠ASB=
如图，已知圆O的弦AB经过弦CD的中点P，若AP=2cm，CD=6cm，则PB的长为