Question

（1）如图1，在△ABC中，点D、E、Q分别在AB、AC、BC上，且DE//BC，AQ交DE于点P,求证：

（2）如图，△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG,AF分别交DE于M,N两点.
①如图2，若AB=AC=1，直接写出MN的长；
②如图3，求证：MN=DM·EN

Answer 1

（1）证明见解析；（2）①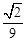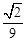，②证明见解析.

试题分析：（1）易证明△ADP∽△ABQ，△ACQ∽△ADP，从而得出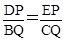.（2）①根据等腰直角三角形的性质和勾股定理，求出BC边上的高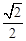，根据△ADE∽△ABC，求出正方形DEFG的边长。从而，由△AMN∽△AGF和△AMN的MN边上高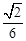，△AGF的GF边上高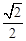，GF=，根据 MN：GF等于高之比即可求出MN. ②可得出△BGD∽△EFC，则DG•EF=CF•BG；又DG=GF=EF，得GF²=CF•BG，再根据（1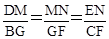），从而得出结论.
试题解析：（1）在△ABQ中，由于DP∥BQ，∴△ADP∽△ABQ.  ∴.
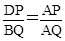同理在△ACQ中，.
∴.
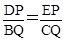（2）① .
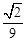②∵∠B+∠C=90°，∠CEF+∠C=90，∴∠B=∠CEF.
又∵∠BGD=∠EFC，∴△BGD∽△EFC.∴.∴DG·EF＝CF·BG.
又∵DG＝GF＝EF，∴GF²＝CF·BG.
由（1）得 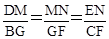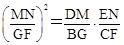，∴. ∴MN²＝DM·EN.