题目内容
 如图,在正方形网格上有△A1B1C1、△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.
如图,在正方形网格上有△A1B1C1、△A2B2C2,这两个三角形相似吗?如果相似,求出△A1B1C1和△A2B2C2的面积比.
解:相似,相似比为2:1, =4:1,
=4:1, =
= =2
=2
通过观察图形发现∠B1A1C1=135°=∠B2A2C2,设每个小方格的边长为1,利用勾股定理可计算A1B1= ,A2B2=
,A2B2= ,A1C1=4,A2C2=2
,A1C1=4,A2C2=2
∴A1B1:A2B2=A1C1:A2C2=2:1,
∴△B1A1C1∽△B2A2C2
∴ =4:1.
=4:1.
分析:通过观察发现∠B1A1C1=135°=∠B2A2C2,若能计算这两角的夹边对应成比例,则两三角形相似,面积比也可求.
点评:此题考查了学生看图分析的能力,主要利用了相似三角形的判定定理及性质.
 =4:1,
=4:1, =
= =2
=2通过观察图形发现∠B1A1C1=135°=∠B2A2C2,设每个小方格的边长为1,利用勾股定理可计算A1B1=
 ,A2B2=
,A2B2= ,A1C1=4,A2C2=2
,A1C1=4,A2C2=2∴A1B1:A2B2=A1C1:A2C2=2:1,
∴△B1A1C1∽△B2A2C2
∴
 =4:1.
=4:1.分析:通过观察发现∠B1A1C1=135°=∠B2A2C2,若能计算这两角的夹边对应成比例,则两三角形相似,面积比也可求.
点评:此题考查了学生看图分析的能力,主要利用了相似三角形的判定定理及性质.

练习册系列答案
相关题目
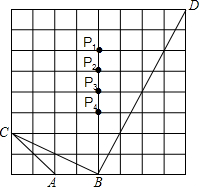 如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.| A、P1 | B、P2 | C、P3 | D、P4 |
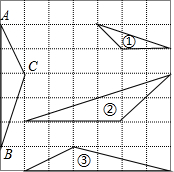 如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有
如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有 如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是
如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是 如图,在正方形网格上有△ABC和△DEF.
如图,在正方形网格上有△ABC和△DEF. 作图计算题.
作图计算题.