题目内容
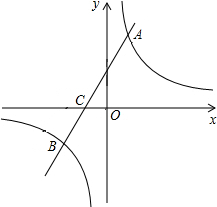 (2013•雅安)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
(2013•雅安)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=| m | x |
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标;
(3)在x轴上求点E,使△ACE为直角三角形.(直接写出点E的坐标)
分析:(1)过点A作AD⊥x轴于D,根据A、C的坐标求出AD=6,CD=n+2,已知tan∠ACO=2,可求出n的值,把点的坐标代入解析式即可求得反比例函数和一次函数解析式;
(2)求出反比例函数和一次函数的另外一个交点即可;
(3)分两种情况:①AE⊥x轴,②EA⊥AC,分别写出E的坐标即可.
(2)求出反比例函数和一次函数的另外一个交点即可;
(3)分两种情况:①AE⊥x轴,②EA⊥AC,分别写出E的坐标即可.
解答: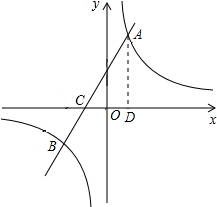 解:(1)过点A作AD⊥x轴于D,
解:(1)过点A作AD⊥x轴于D,
∵C的坐标为(-2,0),A的坐标为(n,6),
∴AD=6,CD=n+2,
∵tan∠ACO=2,
∴
=
=2,
解得:n=1,
故A(1,6),
∴m=1×6=6,
∴反比例函数表达式为:y=
,
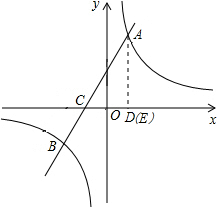
又∵点A、C在直线y=kx+b上,
∴
,
解得:
,
∴一次函数的表达式为:y=2x+4;
(2)由
得:
=2x+4,
解得:x=1或x=-3,
∵A(1,6),
∴B(-3,-2);
(3)分两种情况:①当AE⊥x轴时,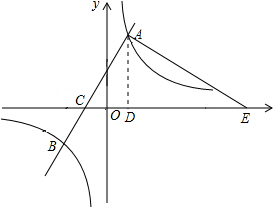
即点E与点D重合,
此时E1(1,0);
②当EA⊥AC时,
此时△ADE∽△CDA,
则
=
,
DE=
=12,
又∵D的坐标为(1,0),
∴E2(13,0).
 解:(1)过点A作AD⊥x轴于D,
解:(1)过点A作AD⊥x轴于D,∵C的坐标为(-2,0),A的坐标为(n,6),
∴AD=6,CD=n+2,
∵tan∠ACO=2,
∴
| AD |
| CD |
| 6 |
| n+2 |
解得:n=1,
故A(1,6),
∴m=1×6=6,
∴反比例函数表达式为:y=
| 6 |
| x |
又∵点A、C在直线y=kx+b上,
∴
|

解得:
|
∴一次函数的表达式为:y=2x+4;
(2)由
|
| 6 |
| x |
解得:x=1或x=-3,
∵A(1,6),
∴B(-3,-2);
(3)分两种情况:①当AE⊥x轴时,

即点E与点D重合,
此时E1(1,0);
②当EA⊥AC时,
此时△ADE∽△CDA,
则
| AD |
| CD |
| DE |
| AD |
DE=
| 36 |
| 3 |
又∵D的坐标为(1,0),
∴E2(13,0).
点评:本题考查了反比例函数的综合题,涉及了点的坐标的求法以及待定系数法求函数解析式的知识,主要考查学生的计算能力和观察图形的能力.

练习册系列答案
相关题目
 (2013•雅安)如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为( )
(2013•雅安)如图,DE是△ABC的中位线,延长DE至F使EF=DE,连接CF,则S△CEF:S四边形BCED的值为( )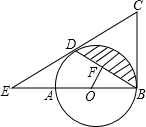 (2013•雅安)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(2013•雅安)如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.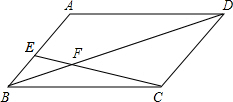 (2013•雅安)如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF=
(2013•雅安)如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF=