题目内容
先阅读材料:“试判断20001999+19992000的末位数字”.
解:∵20001999的末位数字是零,而19992的末位数字是1,
则19992000=(19992)1000的末位数字是1,
∴20001999+19992000的末位数字是1.
同学们,根据阅读材料,你能否判断22013+72013的末位数字是多少?
解:71的末位数字是7,
72的末位数字是9,
73的末位数字是3,
74的末位数字是1,
75的末位数字是7,
…
2013÷4=503…1,
所以72013的末位数字是7;
21的末位数字是2,
22的末位数字是4,
23的末位数字是8,
24的末位数字是6,
25的末位数字是2,
…
2013÷4=503…1,
所以22013的末位数字是2;
所以22013+72013的末位数字是7+2=9.
分析:分别探讨22013和72013的末位数字,进一步得出两个幂和的末位数字即可.
点评:此题考查幂的末位数字,注意从最简单的数字考虑,找出规律解决问题.
72的末位数字是9,
73的末位数字是3,
74的末位数字是1,
75的末位数字是7,
…
2013÷4=503…1,
所以72013的末位数字是7;
21的末位数字是2,
22的末位数字是4,
23的末位数字是8,
24的末位数字是6,
25的末位数字是2,
…
2013÷4=503…1,
所以22013的末位数字是2;
所以22013+72013的末位数字是7+2=9.
分析:分别探讨22013和72013的末位数字,进一步得出两个幂和的末位数字即可.
点评:此题考查幂的末位数字,注意从最简单的数字考虑,找出规律解决问题.

练习册系列答案
相关题目
 与
与 的大小关系,并加以说明.
的大小关系,并加以说明. ,再
,再 ,要判断y的符号可借助函数
,要判断y的符号可借助函数 ,
, .
. 与
与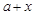 的大小关系,并加以说明.
的大小关系,并加以说明. ,再
,再 ,要判断y的符号可借助函数
,要判断y的符号可借助函数 ,
, .
.