题目内容
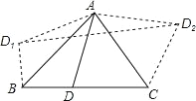
【题目】已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,设AM=x,BN=y,记△ADM的面积为S1,△BND的面积为S2.
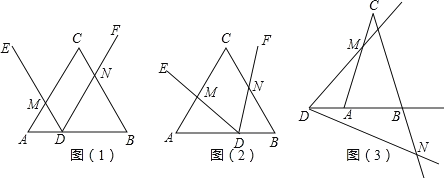
(1)如图(1),当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,S1S2= ;
(2)在(1)的条件下,将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转如图(2)所示位置,
①求y与x的函数关系式;②求S1S2的值;
(3)当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α,如图(3),当点D在BA的延长线上运动时,设的AD=a,BD=b,直接写出S1S2的关系式(用含a、b和α的三角函数表示)
【答案】(1)12;(2)①![]() ;②12;(3)S1S2
;②12;(3)S1S2![]() a2b2sin2α.
a2b2sin2α.
【解析】
(1)首先证明△ADM,△BDN都是等边三角形,可得S1=![]() ,由此即可解决问题.
,由此即可解决问题.
(2)①如图2中,首先证明△AMD∽△BDN,可得![]() ,推出
,推出![]() ,推出xy=8.②由S1=
,推出xy=8.②由S1=![]() ADAMsin60°=
ADAMsin60°=![]() x,S2=
x,S2=![]() DBBNsin60°=
DBBNsin60°=![]() y,可得S1S2=
y,可得S1S2=![]() x
x![]() y=
y=![]() xy=12.
xy=12.
(3)如图3中,设AM=x,BN=y,同法可证△AMD∽△BDN,可得xy=ab,由S1=![]() ADAMsinα=
ADAMsinα=![]() axsinα,S2=
axsinα,S2=![]() DBBNsinα=
DBBNsinα=![]() bysinα,可得S1S2=
bysinα,可得S1S2=![]() (ab)2sin2α.
(ab)2sin2α.
(1)如图1中,
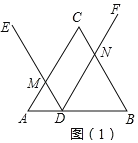
∵△ABC是等边三角形,
∴AB=CB=AC=6,∠A=∠B=60°.
∵DE∥BC,∠EDF=60°,
∴∠BND=∠EDF=60°,
∴∠BDN=∠ADM=60°,
∴△ADM,△BDN都是等边三角形,
∴S1![]() 22
22![]() ,S2
,S2![]() 42=4
42=4![]() ,
,
∴S1S2=12.
故答案为:12.
(2)如图2中,
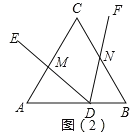
①∵AM=x,BN=y,∠MDB=∠MDN+∠NDB=∠A+∠AMD,∠MDN=∠A,∴∠AMD=∠NDB.
∵∠A=∠B,
∴△AMD∽△BDN,
∴![]() ,
,
∴![]() ,
,
∴xy=8,
②∵S1![]() ADAMsin60°
ADAMsin60°![]() x,S2
x,S2![]() DBBNsin60°
DBBNsin60°![]() y,
y,
∴S1S2![]() x
x![]() y
y![]() xy=12.
xy=12.
(3)如图3中,
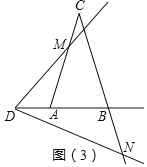
∵AM=x,BN=y,同法可证△AMD∽△BDN,可得xy=ab.
∵S1![]() ADAMsinα
ADAMsinα![]() axsinα,S2
axsinα,S2![]() DBBNsinα
DBBNsinα![]() bysinα,
bysinα,
∴S1S2![]() (ab)2sin2α.
(ab)2sin2α.

【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .