题目内容
已知：如图，若∠DCB=∠A，且BD=2，AD=3，求BC的长．
【答案】分析：利用有两对角相等的两个三角形相似可判定△ABC∽△CBD，再根据相似三角形的性质；对应边的比值相等即可求出BC的长．
解答：解：∵∠B=∠B，∠DCB=∠A，
∴△ABC∽△CBD，
∴
，
∵BD=2，AD=3，
∴
，
∴BC=
．
点评：本题考查了相似三角形的性质和相似三角形的判定，解本题的关键是挖掘出隐藏条件：公共角（∠B=∠B）．
解答：解：∵∠B=∠B，∠DCB=∠A，
∴△ABC∽△CBD，
∴
，∵BD=2，AD=3，
∴
，∴BC=
．点评：本题考查了相似三角形的性质和相似三角形的判定，解本题的关键是挖掘出隐藏条件：公共角（∠B=∠B）．
练习册系列答案
相关题目
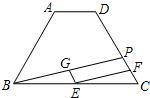，点E、F、G分别是线段BC、PC、BP的中点．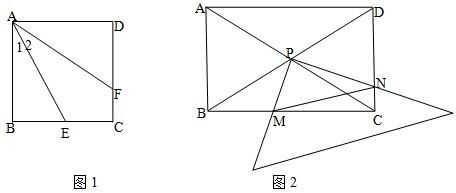
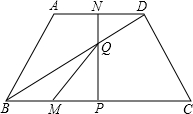的速度向点B运动．若点M、N同时开始运动，其中一点到达终点，另一点也停止运动，运动时间为t（t＞0）．过点N作NP⊥BC与P，交BD于点Q．
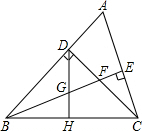已知：如图，在△ABC中，∠ABC=45°，CD⊥AB于点D，BE平分∠ABC，且BE⊥AC于点E，与CD相交于点F．H是BC边的中点，连接DH与BE相交于点G．