Question

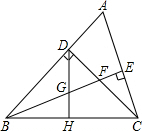已知：如图，在△ABC中，∠ABC=45°，CD⊥AB于点D，BE平分∠ABC，且BE⊥AC于点E，与CD相交于点F．H是BC边的中点，连接DH与BE相交于点G．
（1）求证：△ABC是等腰三角形；
（2）若过点G作GM∥BC，交DC于点M，其他条件不变，求证：DF=CM；
（3）若把题目中“BE平分∠ABC”改为“BE平分线段DC”，其他条件不变，连接HF．求证：HF=AD．

Answer 1

分析：（1）根据角平分线的定义可得∠ABE=∠CBE，根据等角的余角相等求出∠A=∠BCA，再根据等角对等边可得AB=BC，从而得证；
（2）过点F作FN⊥BC于N，根据角平分线上的点到角的两边的距离相等可得FD=FN，根据等角的余角相等求出∠2=∠3，然后根据等角对等边可得DG=DF，从而得到DF=FN，再判断出△BDC是等腰直角三角形，再求出∠GDM=∠NFC=45°，然后利用“角边角”证明△DGM和△FNC全等，根据全等三角形对应边相等可得DM=FC，再求出DF=CM即可；
（3）根据直角三角形斜边上的中线等于斜边的一半可得HF=DF，再利用“角角边”证明△ACD和△BFD全等，根据全等三角形对应边相等可得AD=DF，从而得证．

解答：（1）证明：∵BE平分∠ABC，
∴∠ABE=∠CBE，
∵CD⊥AB，
∴∠ABE+∠A=90°，∠CBE+∠ACB=90°，
∴∠A=∠BCA，
∴AB=BC，
∴△ABC是等腰三角形；

（2）证明：如图，过点F作FN⊥BC于N，
∵BE平分∠ABC，
∴FD=FN，
∵∠ABE+∠3=90°，∠CBE+∠1=90°，∠1=∠2，
∴∠2=∠3，
∴DG=DF，
∴DF=DF=FN，
∵∠ABC=45°，CD⊥AB，
∴△BDC是等腰直角三角形，
∵DH⊥BC，
∴∠GDM=∠NFC=45°，
在△DGM和△FNC中，

∠GDM=∠NFC DG=FN ∠DGM=∠FNC

，
∴△DGM≌△FNC（ASA），
∴DM=FC，
∴DM-FM=FC-FM，
即DF=CM；

（3）证明：如图，连接FH，∵DH⊥BC，BE平分线段CD，
∴HF=DF=

1

2

CD，
∵△BCD是等腰直角三角形，
∴BD=CD，
∵BE⊥AC，
∴∠DBF+∠A=90°，
∵CD⊥AB，
∴∠ACD+∠A=90°，
∴∠DBF=∠ACD，
在△ACD和△BFD中，

∠DBF=∠ACD BD=CD ∠BDF=∠ADC=90°

，
∴△ACD≌△BFD（ASA），
∴AD=DF，
∴HF=AD．

点评：本题考查了全等三角形的判定与性质，等腰直角三角形的判定与性质，直角三角形斜边上的中线等于斜边的一半的性质，平行线的性质，熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形是解题的关键．