题目内容
在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)(a﹣b)=c2,则( )
A.∠A为直角 B.∠C为直角
C.∠B为直角 D.不是直角三角形
A【考点】勾股定理的逆定理.
【专题】探究型.
【分析】先把等式化为a2﹣b2=c2的形式,再根据勾股定理的逆定理判断出此三角形的形状,进而可得出结论.
【解答】解:∵(a+b)(a﹣b)=c2,
∴a2﹣b2=c2,即c2+b2=a2,故此三角形是直角三角形,a为直角三角形的斜边,
∴∠A为直角.
故选A.
【点评】本题考查的是勾股定理的逆定理,即如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
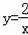
 (x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则
(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴.将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则



 |+2(
|+2(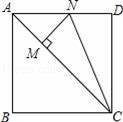


 >
>

 +3
+3








