Question

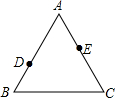如图，在边长为11cm的等边△ABC中，点D、E分别在边AB、AC上，BD=4cm，CE=6cm．在BC边上是否存在一点P，使以点P、B、D为顶点的三角形与以点P、C、E为顶点的三角形相似？如存在，请求出这两个三角形的面积比；如不存在，请说明理由．

Answer 1

分析：存在．设点P在BC上，BP=x，PC=y，则x+y=11，△BPD∽△CEP或△BPD∽△CPE，分两种情况分别求x、y的值，再根据相似三角形的面积比等于相似比的平方求解．

解答：解：存在点P，使以点P、B、D为顶点的三角形与以点P、C、E为顶点的三角形相似．
设点P在BC上，BP=x，PC=y，则有

x+y=11 4 x = 6 y

（I）或

x+y=11 4 x = y 6 .

（ II）
解（ I）得

x= 22 5 y= 33 5

，
解（ II）得

x1=3 y1=8

或

x2=8 y2=3

，
①当

x= 22 5 y= 33 5

时，S_△PDB：S_△PEC=（2：3）²=4：9；
②当

x=3 y=8

时，S_△PDB：S_△PEC=（4：8）²=1：4；
③当

x=8 y=3

时，S_△PDB：S_△PEC=（4：3）²=16：9．

点评：本题考查了相似三角形的判定与性质．关键是根据两个三角形相似的对应关系分类，分别求x、y的值，再根据相似三角形的性质解题．