题目内容
如图,直线 与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线
与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线 于点D,再以BD为边向上作正方形BDEF.
于点D,再以BD为边向上作正方形BDEF.
(1)求点F的坐标;
(2)设直线OF的解析式为 ,若
,若 ,求x的取值范围.
,求x的取值范围.
(1)(2,6);(2)
解析试题分析:(1)将A(2,0)代入 得
得 ,根据正方形的性质可得BC=OC=AB=OA=2,则在
,根据正方形的性质可得BC=OC=AB=OA=2,则在 中,当
中,当 时,
时, ,即得CD、BD的长,再根据正方形的性质可得BF的长;
,即得CD、BD的长,再根据正方形的性质可得BF的长;
(2)将(1)中求得的点F的坐标代入 ,得
,得 ,由
,由 可得关于x的不等式.
可得关于x的不等式.
(1)将A(2,0)代入 得:
得:
∵四边形OABC是正方形
∴BC=OC=AB=OA=2
在 中,当
中,当 时,
时,
∴CD=6
∴BD=CD-BC=6-2=4
∵四边形BDEF是正方形
∴BF=BD=4
∴AF=AB+BF=2+4=6
∴点F的坐标为(2,6);
(2)将F(2,6)代入 ,得
,得
∵
∴
解得 .
.
考点:待定系数法求函数关系式,正方形的性质
点评:待定系数法求函数关系式是初中数学的重点,在中考中极为常见,一般难度不大,需熟练掌握.

练习册系列答案
相关题目

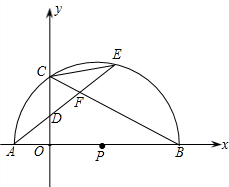 与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.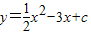 交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.
交x轴正半轴于A、B两点,交y轴于C点,过A、B、C三点作⊙D.若⊙D与y轴相切.
 =
=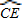 ,
, ,tan∠ECB=
,tan∠ECB= ,求经过A、B、C三点的抛物线的解析式;
,求经过A、B、C三点的抛物线的解析式; AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.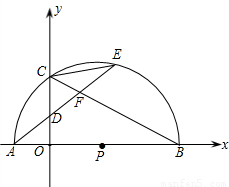
 与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线
与x轴正半轴交于点A(2,0),以OA为边在x轴上方作正方形OABC,延长CB交直线 于点D,再以BD为边向上作正方形BDEF.
于点D,再以BD为边向上作正方形BDEF.
 ,若
,若 ,求x的取值范围.
,求x的取值范围.