题目内容
Rt△ABC中，若∠C=90°，a=15，b=8，则 sinA+sinB=________．
分析：根据勾股定理求出斜边的长，再分别求出∠A，∠B的正弦值，然后求出它们的和即可．
解答：由勾股定理有：c=
=
=17，于是sinA=
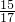；sinB=
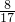，所以sinA+sinB=
．故答案是：
．点评：考查的是锐角三角函数的定义的相关计算；掌握一个角的正弦值等于这个角的对边与斜边之比是解决本题的关键．
练习册系列答案
互动英语系列答案
相关题目
下列说法正确的是（ ）
A、在Rt△ABC中，若tanA=
| ||||
| B、在△ABC中，若a=3，b=4，则tanA=15 | ||||
| C、在Rt△ABC中，∠C=90°，则sin2A+sin2B=1 | ||||
D、tan75°=tan（45°+30°）=tan45°+tan30°=1+
|
在Rt△ABC中，若AC=
，BC=
，AB=3，则下列结论中正确的是（ ）
| 2 |
| 7 |
| A、∠C=90° |
| B、∠B=90° |
| C、△ABC是锐角三角形 |
| D、△ABC是钝角三角形 |
在Rt△ABC中，若各边的长度同时都扩大2倍，则锐角A的正切值（ ）
| A、也扩大2倍 | B、也缩小2倍 | C、不变 | D、扩大1倍 |
如图，Rt△A′BC′是由Rt△ABC绕B点顺时针旋转而得，且点A、B、C′在同一条直线上，在Rt△ABC中，若∠C=90°，BC=2，AB=4，则斜边AB旋转到A′B所扫过的扇形面积为