题目内容
下列说法正确的是( )
A、在Rt△ABC中,若tanA=
| ||||
| B、在△ABC中,若a=3,b=4,则tanA=15 | ||||
| C、在Rt△ABC中,∠C=90°,则sin2A+sin2B=1 | ||||
D、tan75°=tan(45°+30°)=tan45°+tan30°=1+
|
分析:根据三角函数的定义及相关角的三角函数之间的关系综合解答.
解答:解:在Rt△ABC中,若tanA=
,则a=3x,b=4x,x≠0,故A错误,
在△ABC中,若a=3,b=4,则tanA=15,没有说明三角形的形状,故B错误,
在Rt△ABC中,∠C=90°,则sin2A+sin2B=1,sinB=cosA,故C正确,
tan75°=tan(45°+30°)=
=
,故D错误,
故选C.
| 3 |
| 4 |
在△ABC中,若a=3,b=4,则tanA=15,没有说明三角形的形状,故B错误,
在Rt△ABC中,∠C=90°,则sin2A+sin2B=1,sinB=cosA,故C正确,
tan75°=tan(45°+30°)=
1+
| ||||
1-
|
3+2
| ||
| 2 |
故选C.
点评:本题主要考查锐角三角函数的定义,比较简单.

练习册系列答案
相关题目
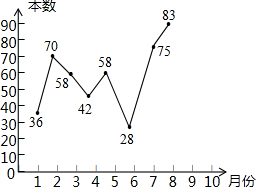 (2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
(2012•东莞模拟)某班去年1~8月“书香校园”活动中全班同学的课外阅读量(单位:本),绘制了如图折线统计图,下列说法正确的是( )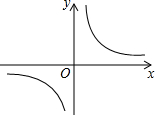 (2013•葫芦岛)如图是反比例函数y=
(2013•葫芦岛)如图是反比例函数y=