Question

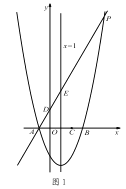
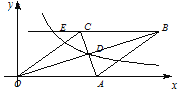
【题目】如图，在直角坐标系中，四边形 OABC 为菱形，对角线 OB、AC 相交于 D 点，已知 A点的坐标为（10，0），双曲线 y=（ x＞0 ）经过 D 点，交 BC 的延长线于 E 点，且 OBAC=120（OB＞AC），有下列四个结论：①双曲线的解析式为y=（x＞0）；②E 点的坐标是（4，6）；③sin∠COA=；④EC=；⑤AC+OB=8．其中正确的结论有（ ）

A. 4 个 B. 3 个 C. 2 个 D. 1 个

Answer 1

【答案】A

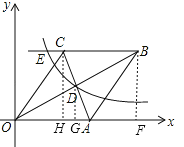
【解析】解：如图，过B作BF⊥x轴于点F，过D作DG⊥x轴于点G，过C作CH⊥x轴于点H．∵A（10，0），∴OA=10，∴S菱形ABCD=OABF=ACOB=×120=60，即10BF=60，∴BF=6．在Rt△ABF中，AB=10，BF=8，由勾股定理可得AF=8，∴OF=OA+AF=10+8=18．∵四边形OABC为菱形，∴D为OB中点，∴DG=BF=×6=3，OG=OF=×18=9，∴D（9，3）．∵双曲线过点D，∴3=，解得：k=27，∴双曲线解析式为y=，故①正确；

∵BC∥OF，BF=6，∴6=，x=，∴E（，6）．故②错误；

在Rt△OCH中，OC=10，CH=6，∴sin∠COA===，故③正确；

∵C（8，6），E（，6），∴EC=8﹣=，故④正确．在Rt△OBF中，OF=18，BF=6，∴OB==6．∵ACOB=120，∴AC==2，∴AC+OB=6+2=8，故⑤正确；

综上可知：正确的为①③④⑤共4个．故选A．