Question

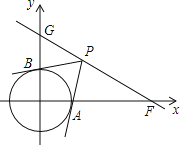
【题目】在平面直角坐标系中，O为坐标原点，已知点F（2，0），直线GF交y轴正半轴于点G，且∠GFO=30°．

（1）直接写出点G的坐标；
（2）若⊙O的半径为1，点P是直线GF上的动点，直线PA、PB分别约⊙O相切于点A、B．
①求切线长PB的最小值；
②问：在直线GF上是够存在点P，使得∠APB=60°，若存在，请求出P点的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）（0，2）；（2）①PB的最小值为；②存在，P点坐标为（0，2）或（，1）．

【解析】

（1）根据含30度的直角三角形的三边的关系得到OG=OF=2，于是得到G点坐标为（0，2）；
（2）连结OA、OB、OP，①由于PB为⊙O的切线，根据切线的性质得OB⊥PB，在Rt△POB中，根据勾股定理得PB=，则当OP最小时，PB最小，此时OP⊥FG，在Rt△OPF中，根据含30度的直角三角形的三边的关系得到OP= ，于是得到PB的最小值为 ；②由于PA、PB为⊙O的切线，根据切线长定理得∠OPB=∠APB=30°，在Rt△OPB中，根据含30度的直角三角形的三边的关系得OP=2OB=2，由于OG=2，所以点P在点G的位置时，满足要求，此时P点坐标为（0，2）；由∠OFG=30°，可得∠OGF=60°，GF=2OG=4，加上OP=OG=2，于是可判断△OPG为等边三角形，则PG=OP=2，可判断点P为GF的中点，然后根据线段的中点坐标公式得到此时P点坐标为（，1）．

（1）∵点F的坐标为（2，0），
∴OF=2，
∵∠GFO=30°，
∴OG=OF=2，
∴G点坐标为（0，2）；
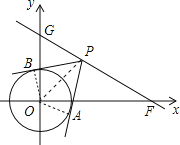
（2）连结OA、OB、OP，如图，
①∵PB为⊙O的切线，
∴OB⊥PB，
∴∠PBO=90°，

在Rt△POB中，OB=1，
∴PB=，
∴当OP最小时，PB最小，
此时OP⊥FG，
在Rt△OPF中，OF=2，∠OFP=30°，
∴OP=，
∴PB的最小值为；
②存在．
∴PA、PB为⊙O的切线，
∴OP平分∠APB，
∴∠OPB=∠APB=×60°=30°，
在Rt△OPB中，OB=1，∠OPB=∠APB=30°，
∴OP=2OB=2，
∵OG=2，
∴点P在点G的位置时，满足要求，此时P点坐标为（0，2）；
∵∠OFG=30°，
∴∠OGF=60°，GF=2OG=4，
∵OP=OG=2，
∴△OPG为等边三角形，
∴PG=OP=2，
∴点P为GF的中点，
∴此时P点坐标为（，1），
综上所述，满足条件的P点坐标为（0，2）或（，1）．