题目内容
已知:ax=5,a2j=3,则ax+4j的值为
- A.15
- B.

- C.45
- D.11
C
分析:根据同底数幂的乘法以及幂的乘方的法则,ax+4j=ax•a4j=ax•(a2j)2,代入数值即可求解.
解答:ax+4j=ax•a4j=ax•(a2j)2=5×32=5×9=45.
故选C.
点评:本题考查了同底数幂的乘法,幂的乘方,理清指数的变化是解题的关键.
分析:根据同底数幂的乘法以及幂的乘方的法则,ax+4j=ax•a4j=ax•(a2j)2,代入数值即可求解.
解答:ax+4j=ax•a4j=ax•(a2j)2=5×32=5×9=45.
故选C.
点评:本题考查了同底数幂的乘法,幂的乘方,理清指数的变化是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
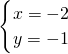 和
和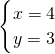 .
.