题目内容
17.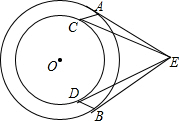 已知两个同心圆,EA、EB是大圆的两条切线,EC、ED是小圆的两条切线,A、B、C、D为切点.求证:AC=BD.
已知两个同心圆,EA、EB是大圆的两条切线,EC、ED是小圆的两条切线,A、B、C、D为切点.求证:AC=BD.
分析 连接OP,根据切线长定理得出AE=BE,CE=DE,∠AEO=∠BEO,∠CEO=∠DEO,进而得出∠AEC=∠BED,然后根据SAS证得△AEC≌△BED,根据全等三角形的性质即可证得结论.
解答 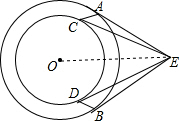 证明:连接OP,
证明:连接OP,
∵两个同心圆,EA、EB是大圆的两条切线,EC、ED是小圆的两条切线,
∴AE=BE,CE=DE,∠AEO=∠BEO,∠CEO=∠DEO,
∴∠AEO-∠CEO=∠BEO-∠DEO,即∠AEC=∠BED,
在△AEC和△BED中
$\left\{\begin{array}{l}{AE=BE}\\{∠AEC=∠BED}\\{CE=DE}\end{array}\right.$
∴△AEC≌△BED(SAS),
∴AC=BD.
点评 本题考查了切线的性质,切线长定理的应用,三角形全等的判定和性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
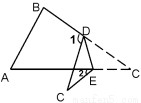
 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( )
ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( )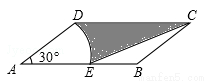
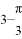 B.
B. 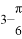 C.
C. 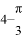 D.
D. 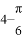
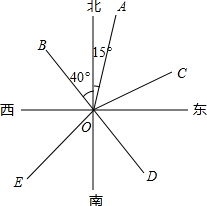 如图,OA的方向是北偏东15°,OB的方向是北偏西40°.
如图,OA的方向是北偏东15°,OB的方向是北偏西40°.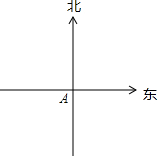 如图,一只渔船从岛A出发沿北偏东30°方向航行了50海里,遇到岛瞧(B点),又沿西北方向航行了25海里(此时记为C点).
如图,一只渔船从岛A出发沿北偏东30°方向航行了50海里,遇到岛瞧(B点),又沿西北方向航行了25海里(此时记为C点).