题目内容
填补下列证明推理的理由
如图,△ABC中,D是边BC的中点,延长AD到点E,且CE∥AB.求证:△ABD≌△ECD
证明:
∵CE∥AB(已知)
∴∠B=∠DCE______
∵D是边BC的中点______
∴BD=CD______
∵AE、BC相交
∴∠ADB=∠EDC______
在△ADB和△EDC中
∠B=∠DCE,BD=CD,∠ADB=∠EDC
∴△ADB≌△EDC______.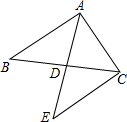
如图,△ABC中,D是边BC的中点,延长AD到点E,且CE∥AB.求证:△ABD≌△ECD
证明:
∵CE∥AB(已知)
∴∠B=∠DCE______
∵D是边BC的中点______
∴BD=CD______
∵AE、BC相交
∴∠ADB=∠EDC______
在△ADB和△EDC中
∠B=∠DCE,BD=CD,∠ADB=∠EDC
∴△ADB≌△EDC______.

证明:∵CE∥AB(已知)
∴∠B=∠DCE (两直线平行,内错角相等).
∵D是边BC的中点 (已知),
∴BD=CD (中点的性质).
∵AE、BC相交
∴∠ADB=∠EDC (对顶角相等),
在△ADB和△EDC中
∠B=∠DCE,BD=CD,∠ADB=∠EDC
∴△ADB≌△EDC( ASA).
故答案分别是:(两直线平行,内错角相等);(已知);(中点的性质);(对顶角相等);(ASA).
∴∠B=∠DCE (两直线平行,内错角相等).
∵D是边BC的中点 (已知),
∴BD=CD (中点的性质).
∵AE、BC相交
∴∠ADB=∠EDC (对顶角相等),
在△ADB和△EDC中
∠B=∠DCE,BD=CD,∠ADB=∠EDC
∴△ADB≌△EDC( ASA).
故答案分别是:(两直线平行,内错角相等);(已知);(中点的性质);(对顶角相等);(ASA).

练习册系列答案
相关题目
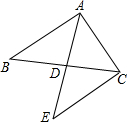 填补下列证明推理的理由
填补下列证明推理的理由

 填补下列证明推理的理由
填补下列证明推理的理由