题目内容
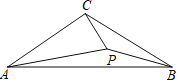
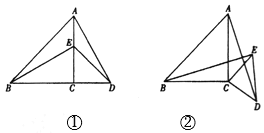
【题目】如图①,在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上任意一点(点
上任意一点(点![]() 与点
与点![]() ,
,![]() 不重合),以
不重合),以![]() 为一直角边作
为一直角边作![]() ,
,![]() ,连接
,连接![]() ,
,![]() .若
.若![]() 和
和![]() 是等腰直角三角形.
是等腰直角三角形.
(1)猜想线段![]() ,
,![]() 之间的数量关系及所在直线的位置关系,直接写出结论;
之间的数量关系及所在直线的位置关系,直接写出结论;
(2)现将图①中的![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,得到图②,请判断(1)中的结论是否仍然成立,若成立,请证明;若不成立,请说明理由.
,得到图②,请判断(1)中的结论是否仍然成立,若成立,请证明;若不成立,请说明理由.
【答案】(1)BE=AD,BE⊥AD ;(2)BE=AD,BE⊥AD仍然成立,理由见解析
【解析】
(1)由CA=CB,CE=CD,∠ACB=90°易证△BCE≌△ACD,所以BE=AD,∠BEC=∠ADC,又因为∠EBC+∠BEC=90°,所以∠EBC+∠ADC=90°,即BE⊥AD;
(2)成立.设BE与AC的交点为点F,BE与AD的交点为点G,易证△ACD≌△BCE.得到AD=BE,∠CAD=∠CBE.再根据等量代换得到∠AFG+∠CAD=90°.即BE⊥AD.
(1)BE=AD,BE⊥AD;
在△BCE和△ACD中,
∵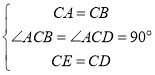 ,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠BEC=∠ADC,
∵∠EBC+∠BEC=90°,
∴∠EBC+∠ADC=90°,
∴BE⊥AD.
故答案为:BE=AD,BE⊥AD.
(2)BE=AD,BE⊥AD仍然成立
设BE与AC的交点为F,BE与AD的交点为G,如图
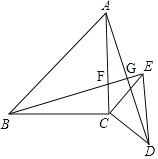
∴![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
∵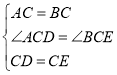
∴![]() .
.
∴![]()
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴BE⊥AD

 阅读快车系列答案
阅读快车系列答案【题目】超市有![]() ,
,![]() 两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买
两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,且无剩油);当日促销活动:购买![]() 型瓶3个或以上,一次性返还现金5元,设购买
型瓶3个或以上,一次性返还现金5元,设购买![]() 型瓶
型瓶![]() (个),所需总费用为
(个),所需总费用为![]() (元),则下列说法不一定成立的是( )
(元),则下列说法不一定成立的是( )
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
A.购买![]() 型瓶的个数是
型瓶的个数是![]() 为正整数时的值B.购买
为正整数时的值B.购买![]() 型瓶最多为6个
型瓶最多为6个
C.![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() D.小张买瓶子的最少费用是28元
D.小张买瓶子的最少费用是28元