题目内容
若x，y，z满足（x-y）2+（z-y）2+2y2-2（x+z）y+2xz=0，且x，y，z是周长为48的一个三角形的三条边长，求y的长．
∵（x-y）2+（z-y）2+2y2-2（x+z）y+2xz
=（x-y）2+（z-y）2+2y2-2xy-2yz+2xz
=（x-y）2+（z-y）2+2y（y-x）-2z（y-x）
=（x-y）2+（z-y）2+2（y-x）（y-z）=0，
=[（x-y）+（z-y）]2=0，即x-y+z-y=0，
∴x+z=2y，
又∵x+y+z=48，
∴2y+y=48，即3y=48，
则y=16．
=（x-y）2+（z-y）2+2y2-2xy-2yz+2xz
=（x-y）2+（z-y）2+2y（y-x）-2z（y-x）
=（x-y）2+（z-y）2+2（y-x）（y-z）=0，
=[（x-y）+（z-y）]2=0，即x-y+z-y=0，
∴x+z=2y，
又∵x+y+z=48，
∴2y+y=48，即3y=48，
则y=16．
练习册系列答案
相关题目
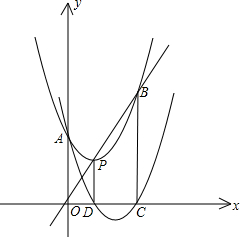如图，抛物线F：y=ax2+bx+c的顶点为P，抛物线F与y轴交于点A，与直线OP交于点B．过点P作PD⊥x轴于点D，平移抛物线F使其经过点A、D得到抛物线F′：y=a′x2+b′x+c′，抛物线F′与x轴的另一个交点为C．