题目内容
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[50°,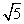 ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
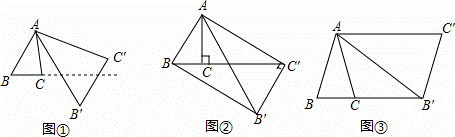
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上, 且四边形ABB'C'为矩形,求θ和n的值;
且四边形ABB'C'为矩形,求θ和n的值;
(4)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
(1). 5; 50° 
(2). θ=∠CAC'=∠BAC'﹣∠BAC=90°﹣30°=60°.
在 Rt△ABC 中,∠ABB'=90°,∠BAB'=60°∴∠AB'B=30°,
∴n=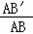 =2;
=2;
(3)∵四边形ABB'C'是平行四边形,∴AC'∥BB',又∵∠BAC=36°,
∴θ=∠CAC'=∠ACB=72°. 
∴∠C'AB'=∠BAC=36°,而∠B=∠B,∴△ABC∽△B'BA,
∴AB:BB'=CB:AB, ∴AB2=CB·BB'=CB(BC+CB'),
而 CB'=AC=AB=B'C', BC=1, ∴AB2=1(1+AB), ∴AB=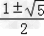 ,
,
∵AB>0, ∴n=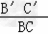 =
=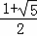 .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 度数为( )
度数为( )

 在第一象限的图象如图所示,点A在其图象上,点B为
在第一象限的图象如图所示,点A在其图象上,点B为 轴正半轴上一点,连接AO、AB,且AO=AB,则S⊿AOB= .
轴正半轴上一点,连接AO、AB,且AO=AB,则S⊿AOB= .
 AB与量角器的直径重合,点D对应54°,则∠BCD
AB与量角器的直径重合,点D对应54°,则∠BCD

 D.
D. 江全长约为6300千米,用科学记数法表示为 千米.
江全长约为6300千米,用科学记数法表示为 千米.