ΧβΡΩΡΎ»ί
»γΆΦΘ§ΨΊ–ΈOABCΘ§AΘ®5Θ§0Θ©Θ§CΘ®0Θ§3Θ©Θ°÷±œΏy=kxΫΜ’έœΏA-B-C”ΎΒψPΘ§ΒψAΙΊ”ΎOPΒΡΕ‘≥ΤΒψAΓδ
Θ®1Θ©Β±AΓδ«ΓΚΟ‘ΎCB±Ώ…œ ±Θ§C AΓδ=
Θ®2Θ©k=
±Θ§Ψ≠ΙΐOΓΔAΓΔAΓδΒΡ≈ΉΈοœΏ«ΓΚΟ“‘AΓδΈΣΕΞΒψΘ§ΗΟ≈ΉΈοœΏΒΡΫβΈω Ϋ «
Θ®3Θ©»τP‘ΎAB±Ώ…œΘ§AΓδ‘ΎCB…œΖΫ ±Θ§AΓδOΓΔAΓδPΫΜCB±Ώ”ΎΒψEΘ§FΘ°«σkΈΣΚΈ÷Β ±ΓςAΓδEFΓ’ΓςBPFΘΩ≤ΔΥΒΟςάμ”…Θ°
Θ®4Θ©“‘OPΈΣ÷±ΨΕΉςΓ―MΘ§‘ρΓ―M”κΨΊ–ΈOABCΉνΕύ”–
ΘΦkΘΦ
«“kΓΌ
ΘΦkΘΦ
«“kΓΌ
Θ®÷±Ϋ”–¥¥πΑΗΘ©

Θ®1Θ©Β±AΓδ«ΓΚΟ‘ΎCB±Ώ…œ ±Θ§C AΓδ=
4
4
Θ§k=| 1 |
| 3 |
| 1 |
| 3 |
Θ®2Θ©k=
| ||
| 3 |
| ||
| 3 |
y=-
x(x-5)Μρy=-
(x-
)2+
| 2 |
| 5 |
| 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
y=-
x(x-5)Μρy=-
(x-
)2+
| 2 |
| 5 |
| 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
Θ®3Θ©»τP‘ΎAB±Ώ…œΘ§AΓδ‘ΎCB…œΖΫ ±Θ§AΓδOΓΔAΓδPΫΜCB±Ώ”ΎΒψEΘ§FΘ°«σkΈΣΚΈ÷Β ±ΓςAΓδEFΓ’ΓςBPFΘΩ≤ΔΥΒΟςάμ”…Θ°
Θ®4Θ©“‘OPΈΣ÷±ΨΕΉςΓ―MΘ§‘ρΓ―M”κΨΊ–ΈOABCΉνΕύ”–
6
6
ΗωΙΪΙ≤ΒψΘ§≤Δ–¥≥ωΙΪΙ≤ΒψΗω ΐΉνΕύ ±kΒΡ»Γ÷ΒΖΕΈß| 11 |
| 60 |
| 60 |
| 91 |
| 3 |
| 5 |
| 11 |
| 60 |
| 60 |
| 91 |
| 3 |
| 5 |

Ζ÷ΈωΘΚΘ®1Θ©»γΆΦ1Θ§Ν§Ϋ”OAΓδΘ§AAΓδΘ°…ηAΓδΘ®xΘ§3Θ©Θ°
ΗυΨίΨΊ–ΈΒΡ–‘÷ Θ§ΒψΒΡΉχ±ξ”κΆΦ–ΈΒΡ–‘÷ “‘ΦΑΙ¥Ι…Ε®άμ«σΒΟCAΓδ=4Θ§»ΜΚσΫαΚœAΘ®5Θ§0Θ©«σΒΟAAΓδΒΡ÷–ΒψDΒΡΉχ±ξ «Θ®4.5Θ§1.5Θ©Θ§¥”Εχ«σΒΟkΒΡ÷ΒΘΜ
Θ®2Θ©“ρΈΣΗΟ≈ΉΈοœΏΨ≠ΙΐΒψOΓΔAΘ§Ι Ω……ηΫΜΒψ ΫΚ· ΐΫβΈω Ϋy=axΘ®x-5Θ©Θ®aΘΦ0Θ©Θ°”…ΕΞΒψΉχ±ξΙΪ Ϋ«σΒΟAΓδΒΡΉχ±ξΘ§ΫαΚœ÷αΕ‘≥ΤΒΡ–‘÷ ά¥«σaΒΡ÷ΒΘΜ
Θ®3Θ©ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡΕ‘”Π±ΏœύΒ»ΚΆΕ‘”ΠΫ«œύΒ»ΓΔΙ¥Ι…Ε®άμ“‘ΦΑ’ΐ«–Κ· ΐΒΡΕ®“εά¥«σkΒΡ÷ΒΘ°
Θ®4Θ©ΗυΨίΧβ“βΘ§Μ≠≥ωΆΦ–ΈΘ§ΗυΨίΆΦ–ΈΜΊ¥πΈ ΧβΘ°
ΗυΨίΨΊ–ΈΒΡ–‘÷ Θ§ΒψΒΡΉχ±ξ”κΆΦ–ΈΒΡ–‘÷ “‘ΦΑΙ¥Ι…Ε®άμ«σΒΟCAΓδ=4Θ§»ΜΚσΫαΚœAΘ®5Θ§0Θ©«σΒΟAAΓδΒΡ÷–ΒψDΒΡΉχ±ξ «Θ®4.5Θ§1.5Θ©Θ§¥”Εχ«σΒΟkΒΡ÷ΒΘΜ
Θ®2Θ©“ρΈΣΗΟ≈ΉΈοœΏΨ≠ΙΐΒψOΓΔAΘ§Ι Ω……ηΫΜΒψ ΫΚ· ΐΫβΈω Ϋy=axΘ®x-5Θ©Θ®aΘΦ0Θ©Θ°”…ΕΞΒψΉχ±ξΙΪ Ϋ«σΒΟAΓδΒΡΉχ±ξΘ§ΫαΚœ÷αΕ‘≥ΤΒΡ–‘÷ ά¥«σaΒΡ÷ΒΘΜ
Θ®3Θ©ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡΕ‘”Π±ΏœύΒ»ΚΆΕ‘”ΠΫ«œύΒ»ΓΔΙ¥Ι…Ε®άμ“‘ΦΑ’ΐ«–Κ· ΐΒΡΕ®“εά¥«σkΒΡ÷ΒΘ°
Θ®4Θ©ΗυΨίΧβ“βΘ§Μ≠≥ωΆΦ–ΈΘ§ΗυΨίΆΦ–ΈΜΊ¥πΈ ΧβΘ°
Ϋβ¥πΘΚ ΫβΘΚΘ®1Θ©»γΆΦ1Θ§Ν§Ϋ”OAΓδΘ§AAΓδΘ°…ηAΓδΘ®xΘ§3Θ©Θ®0ΘΦxΘΦ5Θ©Θ°
ΫβΘΚΘ®1Θ©»γΆΦ1Θ§Ν§Ϋ”OAΓδΘ§AAΓδΘ°…ηAΓδΘ®xΘ§3Θ©Θ®0ΘΦxΘΦ5Θ©Θ°
ΓΏ‘ΎΨΊ–ΈOABC÷–Θ§AΘ®5Θ§0Θ©Θ§CΘ®0Θ§3Θ©Θ§
ΓύOA=5Θ§OC=3Θ°
ΓΏΒψA”κΒψAΓδΙΊ”Ύ÷±œΏOPΕ‘≥ΤΘ§
ΓύOAΓδ=OA=5Θ§
Γύ‘ΎRtΓςOCAΓδ÷–Θ§άϊ”ΟΙ¥Ι…Ε®άμ÷ΣΘ§CAΓδ=
=
=4Θ§
Φ¥C AΓδ=4Θ§
ΓύAΓδΘ®4Θ§3Θ©Θ§
ΓύœΏΕΈAAΓδΒΡ÷–ΒψDΒΡΉχ±ξ «Θ®4.5Θ§1.5Θ©‘Ύ÷±œΏOP…œΘ§
Γύk=
=
Θ°
Θ®2Θ©ΓΏΗΟ≈ΉΈοœΏΨ≠ΙΐΒψOΓΔAΘ§
ΓύΩ……ηΫΜΒψ ΫΚ· ΐΫβΈω Ϋy=axΘ®x-5Θ©Θ®aΘΦ0Θ©Θ§Φ¥y=aΘ®x-
Θ©2-
aΘ°
ΓΏΗΟ≈ΉΈοœΏ“‘ΒψAΓδΈΣΕΞΒψΘ§
ΓύAΓδΘ®
Θ§-
aΘ©Θ°
ΓύkAAΓδ=
=
aΘ§œΏΕΈAAΓδΒΡ÷–ΒψΒΡΉχ±ξ «Θ®
Θ§-
aΘ©Θ°
”÷ΓΏΒψA”κΒψAΓδΙΊ”Ύ÷±œΏOPΕ‘≥ΤΘ§
ΓύœΏΕΈAAΓδΒΡ÷–ΒψΒΡΉχ±ξ «Θ®
Θ§-
aΘ©‘Ύ÷±œΏOP…œΘ§
‘ρ
Θ§
ΫβΒΟΘ§
Θ§
ΓύΗΟ≈ΉΈοœΏΒΡΫβΈω Ϋ «y=-
x(x-5)Μρy=-
(x-
)2+
ΘΜ
Θ®3Θ©Β±k=
±Θ§ΓςAΓδEFΓ’ΓςBPFΘ°άμ”…»γœ¬ΘΚ
»γΆΦ2Θ§…ηPΘ®5Θ§yΘ©Θ°ΓΏΒψA”κΒψAΓδΙΊ”Ύ÷±œΏOPΕ‘≥ΤΘ§
ΓύΓςOAPΓ’ΓςOAΓδPΘ§
ΓύAP=AΓδPΘ§OA=OAΓδ=5Θ°
ΓΏΓςAΓδEFΓ’ΓςBPFΘ§
ΓύAΓδF=FBΘ§AΓδE=BPΘ§ΓœAΓδ=ΓœB=90ΓψΘ§ΓœAΓδEF=ΓœBPFΘ§
ΓύΓœCEO=ΓœBPFΘ§
Γύ
Θ§
ΫβΒΟΘ§y=
Θ§‘ρk=
=
ΘΜ
Θ®4Θ©»γΆΦ3Θ§ΉνΕύ”–6ΗωΫΜΒψΘ§kΒΡ»Γ÷ΒΖΕΈß «ΘΚ
ΘΦkΘΦ
«“kΓΌ
Θ°
Β±0ΘΦkΘΦ
±Θ§”–4ΗωΙ≤Ά§Βψ
k=
Μρ
±Θ§”–5ΗωΙ≤Ά§ΒψΘΜ
k=
±Θ§”–4ΗωΙ≤Ά§ΒψΘ°
Ι ¥πΑΗ «ΘΚ4Θ§
ΘΜ
ΘΜk=
Θ§y=-
x(x-5)Μρy=-
(x-
)2+
ΘΜ6Θ§
ΘΦkΘΦ
«“kΓΌ
Θ°
 ΫβΘΚΘ®1Θ©»γΆΦ1Θ§Ν§Ϋ”OAΓδΘ§AAΓδΘ°…ηAΓδΘ®xΘ§3Θ©Θ®0ΘΦxΘΦ5Θ©Θ°
ΫβΘΚΘ®1Θ©»γΆΦ1Θ§Ν§Ϋ”OAΓδΘ§AAΓδΘ°…ηAΓδΘ®xΘ§3Θ©Θ®0ΘΦxΘΦ5Θ©Θ°ΓΏ‘ΎΨΊ–ΈOABC÷–Θ§AΘ®5Θ§0Θ©Θ§CΘ®0Θ§3Θ©Θ§
ΓύOA=5Θ§OC=3Θ°
ΓΏΒψA”κΒψAΓδΙΊ”Ύ÷±œΏOPΕ‘≥ΤΘ§
ΓύOAΓδ=OA=5Θ§
Γύ‘ΎRtΓςOCAΓδ÷–Θ§άϊ”ΟΙ¥Ι…Ε®άμ÷ΣΘ§CAΓδ=
| OAΓδ2-OC2 |
| 52-32 |
Φ¥C AΓδ=4Θ§
ΓύAΓδΘ®4Θ§3Θ©Θ§
ΓύœΏΕΈAAΓδΒΡ÷–ΒψDΒΡΉχ±ξ «Θ®4.5Θ§1.5Θ©‘Ύ÷±œΏOP…œΘ§
Γύk=
| 1.5 |
| 4.5 |
| 1 |
| 3 |
Θ®2Θ©ΓΏΗΟ≈ΉΈοœΏΨ≠ΙΐΒψOΓΔAΘ§
ΓύΩ……ηΫΜΒψ ΫΚ· ΐΫβΈω Ϋy=axΘ®x-5Θ©Θ®aΘΦ0Θ©Θ§Φ¥y=aΘ®x-
| 5 |
| 2 |
| 25 |
| 4 |
ΓΏΗΟ≈ΉΈοœΏ“‘ΒψAΓδΈΣΕΞΒψΘ§
ΓύAΓδΘ®
| 5 |
| 2 |
| 25 |
| 4 |
ΓύkAAΓδ=
-
| ||
|
| 5 |
| 2 |
| 15 |
| 4 |
| 25 |
| 8 |
”÷ΓΏΒψA”κΒψAΓδΙΊ”Ύ÷±œΏOPΕ‘≥ΤΘ§
ΓύœΏΕΈAAΓδΒΡ÷–ΒψΒΡΉχ±ξ «Θ®
| 15 |
| 4 |
| 25 |
| 8 |
‘ρ
|
ΫβΒΟΘ§
|

ΓύΗΟ≈ΉΈοœΏΒΡΫβΈω Ϋ «y=-
| 2 |
| 5 |
| 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
Θ®3Θ©Β±k=
| 3 |
| 7 |
»γΆΦ2Θ§…ηPΘ®5Θ§yΘ©Θ°ΓΏΒψA”κΒψAΓδΙΊ”Ύ÷±œΏOPΕ‘≥ΤΘ§
ΓύΓςOAPΓ’ΓςOAΓδPΘ§
ΓύAP=AΓδPΘ§OA=OAΓδ=5Θ°
ΓΏΓςAΓδEFΓ’ΓςBPFΘ§
ΓύAΓδF=FBΘ§AΓδE=BPΘ§ΓœAΓδ=ΓœB=90ΓψΘ§ΓœAΓδEF=ΓœBPFΘ§
ΓύΓœCEO=ΓœBPFΘ§
Γύ
|
ΫβΒΟΘ§y=
| 15 |
| 7 |
| ||
| 5 |
| 3 |
| 7 |

Θ®4Θ©»γΆΦ3Θ§ΉνΕύ”–6ΗωΫΜΒψΘ§kΒΡ»Γ÷ΒΖΕΈß «ΘΚ
| 11 |
| 60 |
| 60 |
| 91 |
| 3 |
| 5 |
Β±0ΘΦkΘΦ
| 11 |
| 60 |
k=
| 11 |
| 60 |
| 60 |
| 91 |
k=
| 3 |
| 5 |
Ι ¥πΑΗ «ΘΚ4Θ§
| 1 |
| 3 |
| 3 |
| 7 |
| ||
| 3 |
| 2 |
| 5 |
| 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 11 |
| 60 |
| 60 |
| 91 |
| 3 |
| 5 |
ΒψΤάΘΚ±ΨΧβΩΦ≤ιΝΥΕΰ¥ΈΚ· ΐΉέΚœΧβΘ°ΉΔ“βΘ§ΖΫ≥ΧΉιΒΡΫβΖ®ΒΡ”Π”ΟΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ

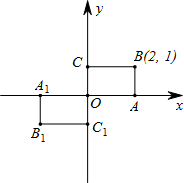 13ΓΔ»γΆΦΘ§ΨΊ–ΈOABCΒΡΕΞΒψOΈΣΉχ±ξ‘≠ΒψΘ§ΒψA‘Ύx÷α…œΘ§ΒψBΒΡΉχ±ξΈΣΘ®2Θ§1Θ©Θ°»γΙϊΫΪΨΊ–Έ0ABC»ΤΒψO–ΐΉΣ180Γψ–ΐΉΣΚσΒΡΆΦ–ΈΈΣΨΊ–ΈOA1B1C1Θ§Ρ«Ο¥ΒψB1ΒΡΉχ±ξΈΣΘ®ΓΓΓΓΘ©
13ΓΔ»γΆΦΘ§ΨΊ–ΈOABCΒΡΕΞΒψOΈΣΉχ±ξ‘≠ΒψΘ§ΒψA‘Ύx÷α…œΘ§ΒψBΒΡΉχ±ξΈΣΘ®2Θ§1Θ©Θ°»γΙϊΫΪΨΊ–Έ0ABC»ΤΒψO–ΐΉΣ180Γψ–ΐΉΣΚσΒΡΆΦ–ΈΈΣΨΊ–ΈOA1B1C1Θ§Ρ«Ο¥ΒψB1ΒΡΉχ±ξΈΣΘ®ΓΓΓΓΘ©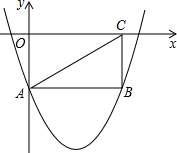 Θ®2012•…ή–ΥΘ©»γΆΦΘ§ΨΊ–ΈOABCΒΡΝΫ±Ώ‘ΎΉχ±ξ÷α…œΘ§Ν§Ϋ”ACΘ§≈ΉΈοœΏy=x2-4x-2Ψ≠ΙΐAΘ§BΝΫΒψΘ°
Θ®2012•…ή–ΥΘ©»γΆΦΘ§ΨΊ–ΈOABCΒΡΝΫ±Ώ‘ΎΉχ±ξ÷α…œΘ§Ν§Ϋ”ACΘ§≈ΉΈοœΏy=x2-4x-2Ψ≠ΙΐAΘ§BΝΫΒψΘ°
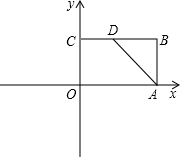 »γΆΦΘ§ΨΊ–ΈOABCΒΡΕΞΒψBΒψΉχ±ξΈΣΘ®3Θ§2Θ©Θ§ΒψD «BCΒΡ÷–ΒψΘ°
»γΆΦΘ§ΨΊ–ΈOABCΒΡΕΞΒψBΒψΉχ±ξΈΣΘ®3Θ§2Θ©Θ§ΒψD «BCΒΡ÷–ΒψΘ°