题目内容
12.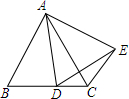 已知△ABC是等边三角形,点D是BC边所在直线上的一个动点,以AD为边,作等边△ADE(点E始终在直线AD的右方),连接CE.
已知△ABC是等边三角形,点D是BC边所在直线上的一个动点,以AD为边,作等边△ADE(点E始终在直线AD的右方),连接CE.(1)当点D在BC边上,求证:BC=DC+CE;
(2)当点D在BC的延长线上时,BC=DC+CE是否成立,请说明理由;
(3)当点D在CB的延长线上时,上述结论是否成立?若不成立,请你画出符合条件的图形,并直接写出成立的结论.
分析 (1)根据等边三角形的性质就可以得出∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE,进而就可以得出△ABD≌△ACE,由△ABD≌△ACE就可以得出BC=DC+CE;
(2)不成立,由等边三角形的性质就可以得出∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE,进而就可以得出△ABD≌△ACE,就可以得出BC+CD=CE;
(3)不成立,由等边三角形的性质就可以得出∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE,进而就可以得出△ABD≌△ACE,就可以得出CE+BC=CD.
解答 解:(1)∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠EAC}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵BC=BD+CD,
∴BC=CE+CD.
(2)不成立,BC+CD=CE成立.
理由如下:
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠EAC}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵BD=BC+CD,
∴CE=BC+CD;
(3)不成立,DC=CE+BC成立.
理由如下:
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC-∠BAE=∠DAE-∠BAE,
∴∠BAD=∠EAC.
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠EAC}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵DC=BD+BC,
∴DC=CE+BC.
符合条件的图形如图所示:
点评 本题考查了等边三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

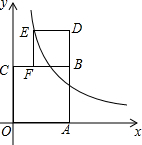 如图,四边形OABC、BDEF是面积分别为S1、S2的正方形,点A在x轴上,点F在BC上,点E在反比例函数y=$\frac{k}{x}$(k>0)的图象上,若S1-S2=2,则k值为( )
如图,四边形OABC、BDEF是面积分别为S1、S2的正方形,点A在x轴上,点F在BC上,点E在反比例函数y=$\frac{k}{x}$(k>0)的图象上,若S1-S2=2,则k值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
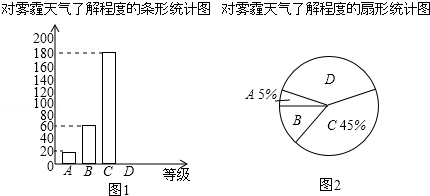
对雾霾了解程度的统计表:
| 对雾霾的了解程度 | 百分比 |
| A.非常了解 | 5% |
| B.比较了解 | m |
| C.基本了解 | 45% |
| D.不了解 | n |
(1)本次参与调查的学生共有400人,m=15%,n=35%;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.