题目内容
4.在下列说法中:①两点确定一条直线;②垂线段最短;③相等的角是对顶角;④三角形三条高、中线、角平分线都分别交于一点,正确的有①②.(只填序号)分析 根据直线的性质可判断①;根据垂线段的性质可判断②;根据对顶角的定义可判断③;根据三角形的高线、中线、角平分线的定义判断即可.
解答 解:①正确;
②正确;
③相等的角不一定是对顶角,故③错误;
④三角形的三条高线所在的直线一定相交于一点,但三条高线不一定相交,故④错误.
故答案为:①②.
点评 本题主要考查的是直线的性质、垂线段的性质、对顶角的定义以及三角形三条高、中线、角平分线的定义,明确角形的三条高线所在的直线一定相交于一点,但三条高线不一定相交是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
15.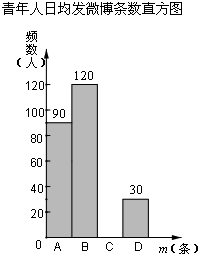 在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:
在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:
青年人日均发微博条数统计表
请你根据以上信息解答下列问题:
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某大城市常住人口中18~35岁的青年人大约有530万人,试估计其中“日均发微博条数”不少于10条的大约有多少万人.
 在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:
在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,15≤m<20时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,根据调查数据整理并制作图表如下:青年人日均发微博条数统计表
| m | 频数 | 百分数 |
| A级(0≤m<5) | 90 | 0.3 |
| B级(5≤m<10) | 120 | a |
| C级(10≤m<15) | b | 0.2 |
| D级(15≤m<20) | 30 | 0.1 |
(1)在表中:a=0.4,b=60;
(2)补全频数分布直方图;
(3)若某大城市常住人口中18~35岁的青年人大约有530万人,试估计其中“日均发微博条数”不少于10条的大约有多少万人.
16.若关于x的不等式组$\left\{\begin{array}{l}{x>3}\\{x<a}\end{array}\right.$无解,则a的取值范围是( )
| A. | a≤3 | B. | a≥3 | C. | a<3 | D. | a>3 |
13.下列标志中不是中心对称图形的是( )
| A. |  中国移动 | B. |  中国银行 | C. |  中国人民银行 | D. |  方正集团 |
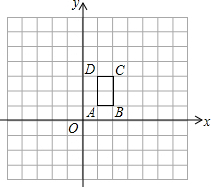 已知:如图,长方形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
已知:如图,长方形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).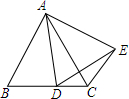 已知△ABC是等边三角形,点D是BC边所在直线上的一个动点,以AD为边,作等边△ADE(点E始终在直线AD的右方),连接CE.
已知△ABC是等边三角形,点D是BC边所在直线上的一个动点,以AD为边,作等边△ADE(点E始终在直线AD的右方),连接CE.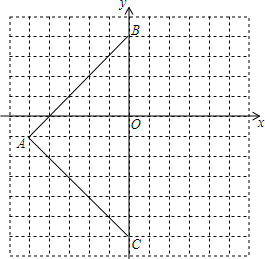 如图,三角形ABC在平面直角坐标系中,三个顶点坐标分别为A(-5,-1)、B(0,4)、C(0,-6).
如图,三角形ABC在平面直角坐标系中,三个顶点坐标分别为A(-5,-1)、B(0,4)、C(0,-6).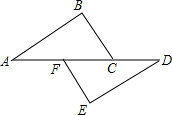 如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且BC∥EF,AF=CD,请你添加一个条件,使得△ABC≌△DEF,并加以证明.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且BC∥EF,AF=CD,请你添加一个条件,使得△ABC≌△DEF,并加以证明. 如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2.