题目内容
| 某工厂计划生产两种产品共10件,其生产成本和利润如下表: |
 |
| (1)若工厂计划获利14万元,问两种产品应分别生产多少件? (2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?哪种方案获利最大?并求最大利润。 |
| 解:(1)设生产A种产品x 件,则生产B种产品(10-x )件 根据题意得:x+2(10-x)=14 解之得:x=6 答:生产A种产品6件,则生产B种产品4件 (2)设生产A种产品y件,则生产B种产品(10-y)件 根据题意得: 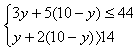 解不等式组得:3≤y<6 因为y为正整数 所以y取3、4、5,则10-y取7、6、5 因此共有三种生产方案,分别如下: 方案一:A种产品3件,B种产品7件; 方案二:A 种产品4 件,B 种产品6 件; 方案三:A 种产品5 件,B 种产品5 件 设工厂获得的利润为w万元, 则w=y+2(10-y)=-y+20 因为-1<0,所以y随x的增大而减小, 所以当y=3时,w的最大值为17万元 答:工厂采用方案一即生产A种产品3件,生产B种产品7件时获得的利润最大,最大利润为17万元。 |

练习册系列答案
相关题目
某工厂计划生产 两种产品共10件,其生产成本和利润如下表:
两种产品共10件,其生产成本和利润如下表:
| |  种产品 种产品 |  种产品 种产品 |
| 成本(万元∕件) | 3 | 5 |
| 利润(万元∕件) | 1 | 2 |
 两种产品应分别生产多少件?
两种产品应分别生产多少件?(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?哪种方案获利最大?并求最大利润.
某工厂计划生产 两种产品共10件,其生产成本和利润如下表:
两种产品共10件,其生产成本和利润如下表:
|
|
|
|
|
成本(万元∕件) |
3 |
5 |
|
利润(万元∕件) |
1 |
2 |
(1)若工厂计划获利14万元,问 两种产品应分别生产多少件?
两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?哪种方案获利最大?并求最大利润.
 种产品
种产品 种产品
种产品 万元;
万元;