题目内容
矩形ABCD的对角线AC,BD相交于点O,AC=4 ,BC=4,在线段AC上取一点E,使△CDE为等腰三角形,请你画出图形,直接写出OE的长,并画出体现解法的辅助线.
,BC=4,在线段AC上取一点E,使△CDE为等腰三角形,请你画出图形,直接写出OE的长,并画出体现解法的辅助线.
【答案】分析:根据矩形的性质以及勾股定理求出AB的长,进而根据当CD=CE时,当ED=CE时求出EO即可.
解答: 解:∵AC=4
解:∵AC=4 ,BC=4,
,BC=4,
∴AB=8,
∵△CDE为等腰三角形,
∴当CD=CE时,EC=CD=8,
∵矩形ABCD的对角线AC,BD相交于点O,AC=4 ,
,
∴AO=CO=2 ,
,
∴EO=AO-AE=AO-(AC-CD)=8-2 ,
,
当ED=CE时,E,O重合,△CED是等腰三角形,此时EO=0.
点评:此题主要考查了应用设计与作图以及矩形的性质和勾股定理,熟练利用矩形性质得出是解题关键.
解答:
 解:∵AC=4
解:∵AC=4 ,BC=4,
,BC=4,∴AB=8,
∵△CDE为等腰三角形,
∴当CD=CE时,EC=CD=8,
∵矩形ABCD的对角线AC,BD相交于点O,AC=4
 ,
,∴AO=CO=2
 ,
,∴EO=AO-AE=AO-(AC-CD)=8-2
 ,
,当ED=CE时,E,O重合,△CED是等腰三角形,此时EO=0.
点评:此题主要考查了应用设计与作图以及矩形的性质和勾股定理,熟练利用矩形性质得出是解题关键.

练习册系列答案
相关题目

 如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为
如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为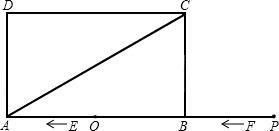 如图,矩形ABCD中,AB=6,BC=2
如图,矩形ABCD中,AB=6,BC=2 已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=5cm,则矩形对角线的长是
已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=5cm,则矩形对角线的长是