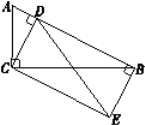
题目内容
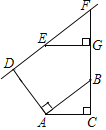
【题目】已知:如图,点E为正方形ABCD边BC上一动点,连接AE,并将线段AE绕点E顺时针旋转90°得到线段EF.过点F作FG⊥BC交BC的延长线于点G.
(1)求证:△ABE≌△EGF;
(2)连接CF,延长FE交AB的延长线于点H.探究线段BH,BC,CF之间的数量关系,并证明你的结论;
(3)连接AF交CD于M,若BH=1,CF=3![]() .求AM的长.
.求AM的长.

【答案】(1)见解析;(2)CF2=2BHBC,理由见解析;(3)![]()
【解析】
(1)根据同角的余角相等得到一对角相等,再由一对直角相等,且AE=EF,利用AAS得到三角形ABE与三角形EFG全等;
(2)结论:CF2=2BHBC.证明△ABE∽△EBH,可得EB2=ABBH,再证明BE=FG=CG即可解决问题.
(3)作FK⊥AB于K,交CD于M.由FN∥AD,推出![]() ,求出AD,FN,AF即可解决问题.
,求出AD,FN,AF即可解决问题.
(1)证明:∵EF⊥AE,
∴∠AEB+∠GEF=90°,
又∵∠AEB+∠BAE=90°
∴∠GEF=∠BAE,
又∵FG⊥BC,
∴∠ABE=∠EGF=90°,
在△ABE与△EGF中,
 ,
,
∴△ABE≌△EGF(AAS);
(2)结论:CF2=2BHBC.
理由:∵∠AEH=∠ABE=∠EBH=90°,
∴∠BAE+∠AEB=90°,∠AEB+∠BEH=90°,
∴∠BEH=∠EAB,
∴△ABE∽△EBH,
∴![]() ,
,
∴EB2=ABBH,
∵△ABE≌△EGF,
∴AB=EG,BE=FG,
∵AB=BC,
∴BC=EG,
∴BE=CG,
∴FG=CG,
∴CF2=FG2+CG2=2FG2,
∴CF2=2BHBC.
(3)作FK⊥AB于K,交CD于M.
∵CF2=2BHBC,CF=3![]() ,BH=1,
,BH=1,
∴BC=9,
∵FG=CG=FN=CN=3,CD=BC=AD=AB=9,
∴AK=DN=6,
在Rt△AKF中,AF=![]() ,
,
∵FN∥AD,
![]()
![]()
![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案【题目】某水果批发市场香蕉的价格如下表
购买香蕉数(千克) | 不超过20千克 | 20千克以上但不超过40千克 | 40千克以上 |
每千克的价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克,已知第二次购买的数量多于第一次购买的数量,共付出264元,请问张强第一次,第二次分别购买香蕉多少千克?