题目内容
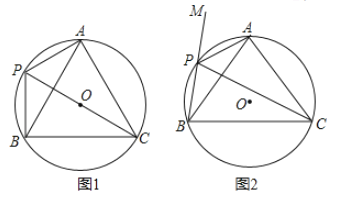
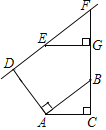
【题目】如图,在Rt△ABC中,∠C=90°,CB=2,CA=4,线段AD由线段AB绕点A逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,当直线EF恰好经过点D时,CG的长等于_____.
【答案】5
【解析】
连接AE,如图,利用勾股定理计算出AB=2![]() ,根据旋转的性质得到∠BAD=90°,AD=AB=2
,根据旋转的性质得到∠BAD=90°,AD=AB=2![]() ,根据平移的性质得到EF∥AB,AE=CG,AE∥CG,接着证明四边形ACGE为矩形得到∠EAC=90°,然后证明Rt△ADE∽Rt△ACB,利用相似比求出AE,从而得到CG的长.
,根据平移的性质得到EF∥AB,AE=CG,AE∥CG,接着证明四边形ACGE为矩形得到∠EAC=90°,然后证明Rt△ADE∽Rt△ACB,利用相似比求出AE,从而得到CG的长.
解:连接AE,如图,
在Rt△ABC中,AB=![]() =2
=2![]() ,
,
∵线段AD由线段AB绕点A逆时针方向旋转90°得到,
∴∠BAD=90°,AD=AB=2![]() ,
,
∵△EFG由△ABC沿CB方向平移得到,当直线EF恰好经过点D时,
∴EF∥AB,AE=CG,AE∥CG,
而∠ACB=90°,
∴四边形ACGE为矩形,
∴∠EAC=90°,
∵FD∥AB,
∴∠ADE=90°,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∴Rt△ADE∽Rt△ACB,
∴![]() ,即
,即![]() ,解得AE=5,
,解得AE=5,
∴CG=5.
故答案为5.


 阅读快车系列答案
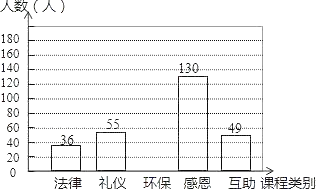
阅读快车系列答案【题目】某校有学生3600人,在“文明我先行”的活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了一些学生,并制成统计表和统计图:
课程类别 | 频数 | 频率 |
法律 | 36 | 0.09 |
礼仪 | 55 | 0.1375 |
环保 | m | a |
感恩 | 130 | 0.325 |
互助 | 49 | 0.1225 |
合计 | n | 1.00 |
(1)在这次调查活动中,学校采取的调查方式是 (填写“普查”或“抽样调查”)a= ,m= ,n= .
(2)请补全条形统计图,如果要画一个“校本课程报名意向扇形统计图”,那么“环保”类校本课程所对应的扇形圆心角应为 度;
(3)请估算该校3600名学生中选择“感恩”校本课程的学生约有多少人?
【题目】北京世界园艺博览会(简称“世园会”)园区4月29日正式开园,门票价格如下:
票种 | 票价(元/人) | |
指定日 | 普通票 | 160 |
优惠票 | 100 | |
平日 | 普通票 | 120 |
优惠票 | 80 | |
注1:“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日),“平日”为世园会会期除“指定日”外的其他日期;
注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票;
注3:提前两天及以上在线上购买世园会门票,票价可打九折,但仅限于普通票.
某大家庭计划在6月1日集体入园参观游览,通过计算发现:若提前两天线上购票所需费用为996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有______人.