题目内容
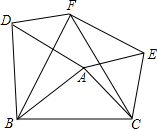如图，以△ABC的各边向同侧作正三角形，即等边△ABD、△BCF、△ACE．求证：四边形AEFD是平行四边形．
分析：根据题中的等式关系可推出两组对边分别相等，从而可判断四边形DAEF为平行四边形．
解答：证明：∵△ABD和△FBC都是等边三角形，
∴∠DBF+∠FBA=∠ABC+∠ABF=60°，BD=BA，BF=BC
∴∠DBF=∠ABC．
∴在△ABC与△DBF中，
∴△ABC≌△DBF（SAS），
∴AC=DF=AE，
同理可证△ABC≌△EFC，
∴AB=EF=AD，
∴四边形DAEF是平行四边形（两组对边分别相等的四边形是平行四边形）．
∴∠DBF+∠FBA=∠ABC+∠ABF=60°，BD=BA，BF=BC
∴∠DBF=∠ABC．
∴在△ABC与△DBF中，
|
∴△ABC≌△DBF（SAS），
∴AC=DF=AE，
同理可证△ABC≌△EFC，
∴AB=EF=AD，
∴四边形DAEF是平行四边形（两组对边分别相等的四边形是平行四边形）．
点评：本题考查了平行四边形的判定、全等三角形的判定与性质以及等边三角形的性质．两组对边分别相等的四边形是平行四边形．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
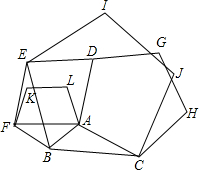（2012•拱墅区一模）如图，以△ABC的各边为边，在BC的同侧分别作三个正五边形．它们分别是正五边形ABFKL、BCJIE、ACHGD，试探究：
如图，以△ABC的各边为边分别向外作正方形，所得到的三个正方形的面积分别为S1=36，S2=64，S3=100，则△ABC的面积是（ ）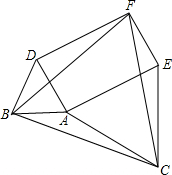
如图，以△ABC的各边为一边向BC的同侧作正△ABD、正△BCF、正△ACE，若∠BAC=150°，求证：四边形AEFD为矩形．
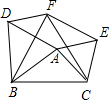如图，以△ABC的各边向同侧作正△ABD，BCF，ACE．