题目内容
如图，点A（x1，y1）、B（x2，y2）都在双曲线y=
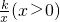上，且x2-x1=4，y1-y2=2．分别过点A、B向x轴、y轴作垂线段，垂足分别为C、D、E、F，AC与BF相交于G点，四边形FOCG的面积为2，五边形AEODB的面积为14，那么双曲线的解析式为
- A.y=
- B.y=
- C.y=
- D.y=
B
分析：根据S矩形AEOC=S矩形OFBD=
（S五边形AEODB-S△AGB-S四边形FOCG）+S四边形FOCG，先求得S矩形AEOC和S矩形OFBD的值，利用k=AE•AC=FB•BD即可求得函数解析式．
解答：∵x2-x1=4，y1-y2=2，
∴BG=4，AG=2，
∴S△AGB=4，
∵S矩形AEOC=S矩形OFBD，四边形FOCG的面积为2，
∴S矩形AEOC=S矩形OFBD=（S五边形AEODB-S△AGB-S四边形FOCG）+S四边形FOCG=（14-4-2）+2=6，
即AE•AC=6，
即可得：y=．
故选B．
点评：此题综合考查了反比例函数与一次函数的性质，此题难度稍大，综合性比较强，注意反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值．
分析：根据S矩形AEOC=S矩形OFBD=
（S五边形AEODB-S△AGB-S四边形FOCG）+S四边形FOCG，先求得S矩形AEOC和S矩形OFBD的值，利用k=AE•AC=FB•BD即可求得函数解析式．解答：∵x2-x1=4，y1-y2=2，
∴BG=4，AG=2，
∴S△AGB=4，
∵S矩形AEOC=S矩形OFBD，四边形FOCG的面积为2，
∴S矩形AEOC=S矩形OFBD=
（S五边形AEODB-S△AGB-S四边形FOCG）+S四边形FOCG=（14-4-2）+2=6，即AE•AC=6，
即可得：y=
．故选B．
点评：此题综合考查了反比例函数与一次函数的性质，此题难度稍大，综合性比较强，注意反比例函数上的点向x轴y轴引垂线形成的矩形面积等于反比例函数的k值．
练习册系列答案
教材全解字词句篇系列答案
相关题目
（2013•历下区二模）如图，点A（x1，y1）、B（x2，y2）都在双曲线y=
如图，点E（x1，y1）、F（x2，y2）在抛物线y=ax2+bx+c的对称轴的同侧 （点E在点F的左侧），过点E、F分别作x轴的垂线，分别交x轴于点B、D，交直线y=2ax+b于点A、C，设S为直线AB、CD与x轴、直线y=2ax+b所围成图形的面积．则S与y1、y2的数量关系式为：S=
如图，点A（x1，y1）、B（x2，y2）都在双曲线y=
如图，点A（x1，y1）、B（x2，y2）在函数y=-| 1 |
| x |
| A、x1＜x2，y1＜y2 |
| B、x1＜x2，y1＞y2 |
| C、x1＞x2，y1＜y2 |
| D、x1＞x2，y1＞y2 |
如图，点P（x1，y1），Q（x2，y2）在直线l上，且x1＞x2，比较y1和y2的大小：