题目内容
（2003•昆明）阅读下列材料：如图表示我国农村居民的小康生活水平实现程度地处西部某贫困县，农村人口约50万，2002年农村小康生活的综合实现程度才达到68%，即没有达到小康程度的人口约为（1-68%）×50万=16万．
解答下列问题：
（1）假设该县计划在2002年的基础上，到2004年底，使没有达到小康程度的16万农村人口降至10.24万，那么平均每年降低的百分率是多少？
（2）如果该计划实现，2004年底该县农村小康进程接近图中哪一年的水平？（假设该县人口2年内不变）
【答案】分析：（1）本题同增长率问题类似，可参照增长率的一般规律进行求解．增长率问题，一般形式为
a（1+x）2=b，a为起始时间的有关数量，b为终止时间的有关数量；
（2）可先计算出2004年底的小康进程，然后同条形图进行比较，得出相近的年份．
解答：解：（1）设平均每年降低的百分率为x，
据题意得：16（1-x）2=10.24，
（1-x）2=0.64，
解得：x1=1.8（不合题意，舍去）x2=0.2．
答：平均每年降低的百分率为20%．
（2）
×100%=79.52%，
答：如果该计划实现，2004年底该县农村小康进程接近1996年全国农村小康进程的水平．
点评：本题考查求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b（当增长时中间的“±”号选“+”，当降低时中间的“±”号选“-”）．
a（1+x）2=b，a为起始时间的有关数量，b为终止时间的有关数量；
（2）可先计算出2004年底的小康进程，然后同条形图进行比较，得出相近的年份．
解答：解：（1）设平均每年降低的百分率为x，
据题意得：16（1-x）2=10.24，
（1-x）2=0.64，
解得：x1=1.8（不合题意，舍去）x2=0.2．
答：平均每年降低的百分率为20%．
（2）
×100%=79.52%，答：如果该计划实现，2004年底该县农村小康进程接近1996年全国农村小康进程的水平．
点评：本题考查求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b（当增长时中间的“±”号选“+”，当降低时中间的“±”号选“-”）．
练习册系列答案
相关题目
阅读下表：
解答下列问题：
（1）在上表中空白处分别画出图形，写出结果；
（2）写出线段的总条数N与线段上的点数n的关系式；
（3）试证明：N=
．
| 线段AB上的点数n（包括A、B两点） | 图例 | 线段总条数N |
| 3 |  |
3=2+1 |
| 4 |  |
6=3+2+1 |
| 5 |  |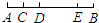
10=4+3+2+1 |
| 6 |  |
15=5+4+3+2+1 |
| 7 |
（1）在上表中空白处分别画出图形，写出结果；
（2）写出线段的总条数N与线段上的点数n的关系式；
（3）试证明：N=
| n(n-1) |
| 2 |
阅读下题的两个解答过程，然后回答问题：
