��Ŀ����
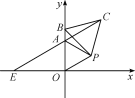
����Ŀ����������y=ax2+c��x�ύ�ڵ�A��m��0����B��n��0������y�ύ�ڵ�C��0��c���������ABCΪ�����������������ر�أ���mnc��0ʱ������ABCΪ��������������������mnc��0ʱ������ABCΪ����������������������ABCΪ����������������ʱ��a��cӦ�ֱ���������_____��_____������ABCΪ��������������������ʱ��ABC�������x�����Գ�ͼ��ǡ�ù�����һ����60���ǵ����Σ���a��cӦ����Ĺ�ϵΪ_____��
���𰸡�a��0�� c��0 ac=��3��![]() ��
��
��������
(1)�����������εĶ����֪����ABCΪ����������������ʱ������������������y�Ḻ�����н�����
(2)����CAB=60������CAB=30����������ֱ����.
����(1)�������֪mn��0����a��0��c��0ʱ��Ϊ��ABCΪ������������������
(2)����CAB=60��ʱ����AO=tan60���c=![]() c����a(
c����a(![]() c)2+c=0����ã�ac=��
c)2+c=0����ã�ac=��![]() ��
��
����CAB=30��ʱ����AO=tan30���c=![]() c����a(
c����a(![]() c)2+c=0����ã�ac=-3��
c)2+c=0����ã�ac=-3��
�ʴ�Ϊ��ac=��3��![]() ��
��

��ϰ��ϵ�д�
 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д� ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
�����Ŀ