Question

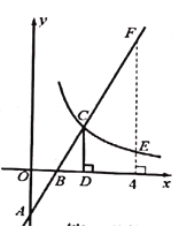
【题目】如图，已知抛物线的顶点为M(2，-4)，且过点A(-1，5)，连接AM交x轴于点B．

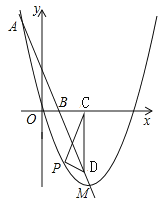
(1)求这条抛物线的解析式；

(2)求点B的坐标；

(3)设点P(x，y)是抛物线在x轴下方、顶点左方一段上的动点，连接PO，过以P为顶角顶点、PO为腰的等腰三角形的另一顶点C作x轴的垂线交直线AM于点D，连结PD，设△PCD的面积为S，求S与x之间的函数关系式；

(4)在上述动点P(x，y)中，是否存在使=2的点?若存在，求点P的坐标；若不存在，说明理由．

Answer 1

【答案】（1）;（2）;（3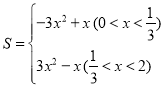） ;（4）存在动点P，使，此时P点坐标为（1，－3）．

【解析】

（1）根据抛物线的顶点为M（2，﹣4），且过点A（﹣1，5），用待定系数法即可求出二次函数的解析式即可；

（2）由于直线AM过A，M两点，可用待定系数法求出直线的解析式，从而求出直线与x轴的交点B的坐标．

（3）设点P（x，y），则C的坐标是（2x，0），把2x代入直线AM的解析式，就可以求出D的坐标．得到CD的长度，CD边上的高是x，因而△PCD的面积就可以用x表示出来，得到S与x的函数解析式．

（4）使S△PCD＝2，把s＝2代入函数的解析式，就可以得到关于x的方程，解方程求解即可．

解：（1）设抛物线的解析式为y＝a(x﹣h)2+k（a≠0），

∵顶点为M（2，﹣4），

∴y＝a(x﹣2)2﹣4，

∵根据抛物线过点A（﹣1，5），

∴5＝a(﹣1﹣2)2﹣4，

解得：a＝1，

∴y＝(x﹣2)2﹣4＝x2﹣4x，

∴这条抛物线的解析式为y＝x2﹣4x；

（2）设直线AM的解析式为y＝kx+b（k≠0），

把M（2，﹣4），A（﹣1，5）两点代入，

得，

解得，

故直线AM的解析式为y＝﹣3x+2，

令y＝0，解得x＝，

故B点坐标为（，0）；

（3）点P（x，y）是抛物线在x轴下方、对称轴左侧部分上的点，

当0＜x＜时，

设P（x，x2﹣4x），

∵以PO、PC为腰的等腰三角形的另一顶点C在x轴上，

∴C的坐标是（2x，0），

∵CD⊥x轴，

∴D（2x，﹣6x+2），

∴CD＝|﹣6x+2|＝﹣6x+2，h＝2x﹣x＝x，

∴S△PCD＝×（﹣6x+2）×x＝﹣3x2+x．

当＜x＜2时，

设P（x，x2﹣4x），

∵以PO、PC为腰的等腰三角形的另一顶点C在x轴上，

∴C的坐标是（2x，0），

∵CD⊥x轴，

∴D（2x，﹣6x+2），

∴CD＝|﹣6x+2|＝6x﹣2，h＝2x﹣x＝x，

∴S△PCD＝×（6x﹣2）×x＝3x2﹣x．

∴S＝；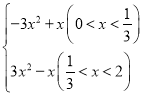

（4）s＝2代入（3）中函数的解析式即可得

2＝﹣3x2+x或2＝3x2﹣x，

当2＝﹣3x2+x，方程的△＜0，方程无解；

当2＝3x2﹣x，解得：x1＝1，x2＝﹣，

当x＝1时y＝x2﹣4x＝﹣3，即抛物线上的P点坐标为（1，﹣3）时，s＝2成立；

当x＝﹣＜0（舍去），

∴存在动点P，使S＝2，此时P点坐标为（1，﹣3）．