题目内容
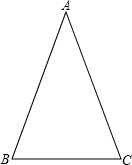
 如图,有一个直角三角形ABC,∠C=90°,AC=12,BC=5,一条线段PO=AB,P、O两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=________时,才能使△ABC与△POA全等.
如图,有一个直角三角形ABC,∠C=90°,AC=12,BC=5,一条线段PO=AB,P、O两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=________时,才能使△ABC与△POA全等.
5或12
分析:要使△ABC≌△POA,根据全等三角形的性质可得AP=CA,则说明当P运动到C时,利用直角三角形全等的判定HL可证△ABC≌△POA.
解答:证明:①当AP=5时,△ABC≌△POA.
∵AX⊥AC,∠C=90°,
∴∠C=∠PAO=90°,
又∵AP=CB=5,PO=AB,
∴△ABC≌△POA;
②当AP=12时,△ABC≌△POA.
∵AX⊥AC,∠C=90°,
∴∠BCA=∠PAO=90°,
又∵AP=CA=12,PO=AB,
∴△ABC≌△POA.
故答案为:5或12.
点评:本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关健.
分析:要使△ABC≌△POA,根据全等三角形的性质可得AP=CA,则说明当P运动到C时,利用直角三角形全等的判定HL可证△ABC≌△POA.
解答:证明:①当AP=5时,△ABC≌△POA.
∵AX⊥AC,∠C=90°,
∴∠C=∠PAO=90°,
又∵AP=CB=5,PO=AB,
∴△ABC≌△POA;
②当AP=12时,△ABC≌△POA.
∵AX⊥AC,∠C=90°,
∴∠BCA=∠PAO=90°,
又∵AP=CA=12,PO=AB,
∴△ABC≌△POA.
故答案为:5或12.
点评:本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.添加时注意:AAA、SSA不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关健.

练习册系列答案
相关题目
 互唯一确定的.
互唯一确定的. .
. .
. .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
 的值为( ▼ )
的值为( ▼ ) B.
1 C.
B.
1 C.  D.
2
D.
2 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ . ,其中
,其中 为锐角,试求sad
为锐角,试求sad .
. .
. .
. .
.