题目内容
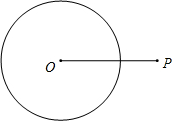 如图,点P在⊙O外.
如图,点P在⊙O外.(1)求作⊙A,使⊙A过O、P两点,且直径等于OP;
(2)设⊙A与⊙O的两个交点分别为点B与点C,则直线PB、PC与⊙O的位置关系是
相切
相切
;线段PB、PC的数量关系是相等
相等
.(直接写出结果)分析:(1)作出线段OP的中垂线,以中垂线与OP的交点为圆心,以
OP为半径画圆即可.
(2)连接OC,OB,根据半径所对的圆周角为直角可判断出PC,PB是⊙O的两条切线,从而可得出答案.
| 1 |
| 2 |
(2)连接OC,OB,根据半径所对的圆周角为直角可判断出PC,PB是⊙O的两条切线,从而可得出答案.
解答:解:(1)①作出线段OP的中垂线,②以中垂线与OP的交点为圆心,以
OP为半径画圆,所作图形如下:

(2)连接OC,OB则可得∠OCP=∠OBP=90°,

从而可得PC,PB是⊙O的两条切线.故可得PB=PC.
故答案为:相切、相等.
| 1 |
| 2 |

(2)连接OC,OB则可得∠OCP=∠OBP=90°,

从而可得PC,PB是⊙O的两条切线.故可得PB=PC.
故答案为:相切、相等.
点评:本题考查了直线与圆的位置关系及复杂作图的知识,难度一般,关键是掌握切线的判定定理及切线的性质,另外要熟练线段中垂线的作法.

练习册系列答案
相关题目

 6、如图,点O在⊙A外,点P在线段OA上运动.以OP为半径的⊙O与⊙A的位置关系不可能是下列中的( )
6、如图,点O在⊙A外,点P在线段OA上运动.以OP为半径的⊙O与⊙A的位置关系不可能是下列中的( )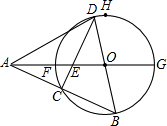 如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,弧FH=弧GH,点D是弧FH上一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=
如图,点A在⊙O外,射线AO与⊙O交于F、G两点,点H在⊙O上,弧FH=弧GH,点D是弧FH上一个动点(不运动至F),BD是⊙O的直径,连接AB,交⊙O于点C,连接CD,交AO于点E,且OA=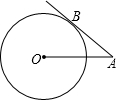 如图,点A在⊙O外,OA=4,⊙O的半径是3,AB切⊙O于点B,则AB的长为
如图,点A在⊙O外,OA=4,⊙O的半径是3,AB切⊙O于点B,则AB的长为