Question

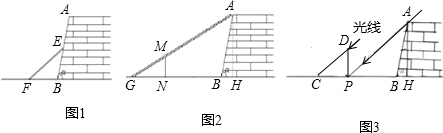
九（1）班数学兴趣小组在社会实践活动中，进行了如下的课题研究：用一定长度的铝合金材料，将它设计成外观为长方形的三种框架，使长方形框架面积最大．
小组讨论后，同学们做了以下三种试验：

请根据以上图案回答下列问题：
（1）在图案1中，如果铝合金材料总长度（图中所有黑线的长度和）为6m，当AB为1m，长方形框架ABCD的面积是______m²；
（2）在图案2中，如果铝合金材料总长度为6m，设AB为xm，长方形框架ABCD的面积为S=______（用含x的代数式表示）；当AB=______m时，长方形框架ABCD的面积S最大；在图案3中，如果铝合金材料总长度为lm，设AB为xm，当AB=______m时，长方形框架ABCD的面积S最大．
（3）经过这三种情形的试验，他们发现对于图案4这样的情形也存在着一定的规律．探索：如图案4如果铝合金材料总长度为lm共有n条竖档时，那么当竖档AB多少时，长方形框架ABCD的面积最大．

Answer 1

【答案】分析：（1）当AB=1时，BC==；长方形框架ABCD的面积是：1×=；
（2）当AB=x时，BC==2-x，长方形框架ABCD的面积为S=x（2-x）=-x²+2x，当x=-=1时，S=-x²+2x=1：在图案3中，如果铝合金材料总长度为lm，设AB为xm，则BC=，S=x•=-x²+x：
当x=-=时，长方形框架ABCD的面积S最大；
（3）如果铝合金材料总长度为lm共有n条竖档时，则BC=，S=x•=-，依照同样方法可求当x=时，长方形框架ABCD的面积最大．
解答：解：（1），（2分）

（2）-x²+2x，1，，（6分）

（3）设AB长为xm，那么AD为，（7分）
S=x•=-，（8分）
当x=时，S最大．（9分）
点评：考查数学活动过程中，学生对活动对象、有关知识与方法的理解，培养探究意识．能通过观察、实验、归纳等获得猜想．