题目内容
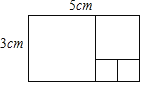
【题目】请将宽为3cm、长为ncm的长方形(n为正整数)分割成若干小正方形,要求小正方形的边长是正整数且个数最少.例如,当n=5cm时,此长方形可分割成如右图的4个小正方形.
请回答下列问题:
(1)n=16时,可分割成几个小正方形?
(2)当长方形被分割成20个小正方形时,求n所有可能的值;
(3)一般地,n>3时,此长方形可分割成多少个小正方形.
【答案】(1)可分割成8个小正方形;(2)n所有可能的值为60或52或53;(3)当n>3时,此长方形可分割成小正方形为:当n=3k时,有k个小正方形;当n═3k+1时,有(k+3)个小正方形;当n=3k+2时,有(k+3)个小正方形.
【解析】
根据题意,继续画图分析并总结规律,然后再解决下列问题即可.
(1)根据以上结论即可求解;
(2)根据以上结论即可求解;
(3)根据总结规律整理到一起即可.
解:若n=4=3×1+1时,如下图所示,此时共有4=(1+3)个小正方形

若n=7=3×2+1时,如下图所示,此时共有5=(2+3)个小正方形

由上可知:当n等于3的k倍加1时,小正方形的个数为(k+3)个,即当n═3k+1时,有(k+3)个小正方形;
若n=5=3×1+2时,如下图所示,此时共有4=(1+3)个小正方形
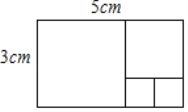
若n=8=3×2+2时,如下图所示,此时共有5=(2+3)个小正方形

由上可知: 当n等于3的k倍加2时,小正方形的个数为(k+3)个,即当 n=3k+2时,有(k+3)个小正方形;
若n=6=3×2时,如下图所示,此时共有2个小正方形

若n=9=3×3时,如下图所示,此时共有3个小正方形

由上可知: 当n等于3的k倍时,小正方形的个数为k个,即 n=3k时,有k个小正方形;
(1)n=16=3×5+1时,可分割成5+3=8个小正方形;
(2)当长方形被分割成20个小正方形时,
若n=3k时,此时k=20,代入解得:n=60;
若n═3k+1时,此时k+3=20,解得k=17,代入解得:n═52;
若n=3k+2时,此时k+3=20,解得k=17,代入解得:n═53.
综上所述:n所有可能的值为60或52或53;
(3)由上可知:当n>3时,此长方形可分割成小正方形为:
当n=3k时,有k个小正方形;
当n═3k+1时,有(k+3)个小正方形;
当n=3k+2时,有(k+3)个小正方形.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
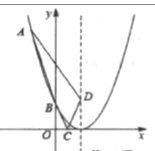
轻巧夺冠周测月考直通高考系列答案【题目】函数y=x2+3x+2的图象如图1所示,根据图象回答问题:
(1)当x满足 时,x2+3x+2>0;
(2)在解决上述问题的基础上,探究解决新问题:
①函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
②下表是函数y=![]() 的几组y与x的对应值.
的几组y与x的对应值.
x | … | ﹣7 | ﹣6 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 3 | 4 | … |
y | … | 5.477 … | 4.472 … | 2.449 … | 1.414 … | 0 | 0 | 1.414 … | 2.449 … | 4.472 … | 5.477 … | … |
如图2,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点的大概位置,请你根据描出的点,画出该函数的图象:
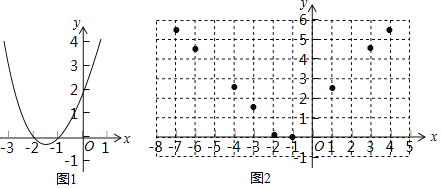
③利用图象,直接写出关于x的方程x4=x2+3x+2的所有近似实数解 (结果精确到0.1)