题目内容
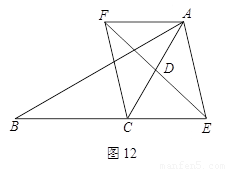
如图12,在△ABC中,∠ACB=![]() ,AC=BC=2,M是边AC的中点,CH⊥BM于H.
,AC=BC=2,M是边AC的中点,CH⊥BM于H.

1.试求sin∠MCH的值
2.求证:∠ABM=∠CAH;
3.若D是边AB上的点,且使△AHD为等腰三角形,请直接写出AD的长为________.
1.![]()
2.见解析
3.![]() 、
、 、
、
解析:(1)在△MBC中,∠MCB=![]() ,BC=2,
,BC=2,
又∵M是边AC的中点,
∴AM=MC=![]() BC=1,
BC=1,
∴MB= ,
,
又CH⊥BM于H,则∠MHC=![]() ,
,
∴∠MCH=∠MBC,
∴sin∠MCH=![]() .
.
(2)在△MHC中, .
.
∴AM2=MC2=![]() ,即
,即![]() ,
,
又∵∠AMH=∠BMA,
∴△AMH∽△BMA,
∴∠ABM=∠CAH.
(3)![]() 、
、![]() 、
、![]()

练习册系列答案
相关题目
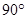 ,AC=BC=2,M是边AC的中点,CH⊥BM于H.
,AC=BC=2,M是边AC的中点,CH⊥BM于H.
 ,AC=BC=2,M是边AC的中点,CH⊥BM于H.
,AC=BC=2,M是边AC的中点,CH⊥BM于H.
 ,AC=BC=2,M是边AC的中点,CH⊥BM于H.
,AC=BC=2,M是边AC的中点,CH⊥BM于H.
 BC ,试判断四边形AFCE是什么样的四边形,并证明你的结论;
BC ,试判断四边形AFCE是什么样的四边形,并证明你的结论;