题目内容
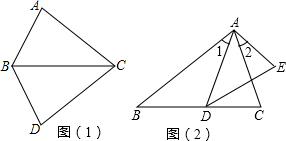 如图(1),∠ABC=∠DBC,请补充一个条件:______,使△ABC≌△DBC.
如图(1),∠ABC=∠DBC,请补充一个条件:______,使△ABC≌△DBC.
如图(2),∠1=∠2,请补充一个条件:______,使△ABC∽△ADE.
解:(1)利用“边角边”可添加:AB=DB,
利用“角角边”可添加:∠A=∠D,
利用“角边角”可添加:∠ACB=∠DCB;
所以,可添加的条件为AB=DB或∠A=∠D或∠ACB=∠DCB;
(2)∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
即∠BAC=∠DAE,
利用“两角对应相等,两三角形相似”可添加:∠C=∠E或∠B=∠ADE,
利用“两边对应成比例,两三角形相似”可添加: =
=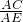 ,
,
所以,可添加的条件为:∠C=∠E或∠B=∠ADE或 =
=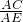 .
.
故答案为:AB=DB或∠A=∠D或∠ACB=∠DCB;∠C=∠E或∠B=∠ADE或 =
=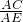 .
.
分析:(1)根据全等三角形的不同判定方法,分情况添加不同的条件;
(2)根据相似三角形的判定方法,分情况添加不同的条件即可.
点评:本题考查了全等三角形的判定,相似三角形的判定,熟练掌握相似三角形的判定方法,全等三角形的判定方法是解题的关键.
利用“角角边”可添加:∠A=∠D,
利用“角边角”可添加:∠ACB=∠DCB;
所以,可添加的条件为AB=DB或∠A=∠D或∠ACB=∠DCB;
(2)∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
即∠BAC=∠DAE,
利用“两角对应相等,两三角形相似”可添加:∠C=∠E或∠B=∠ADE,
利用“两边对应成比例,两三角形相似”可添加:
 =
=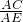 ,
,所以,可添加的条件为:∠C=∠E或∠B=∠ADE或
 =
=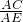 .
.故答案为:AB=DB或∠A=∠D或∠ACB=∠DCB;∠C=∠E或∠B=∠ADE或
 =
=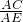 .
.分析:(1)根据全等三角形的不同判定方法,分情况添加不同的条件;
(2)根据相似三角形的判定方法,分情况添加不同的条件即可.
点评:本题考查了全等三角形的判定,相似三角形的判定,熟练掌握相似三角形的判定方法,全等三角形的判定方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD.
已知:如图,等边三角形ABC中,D、E分别是BC、AC上的点,且AE=CD. 如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD.
如图,在等腰直角△ABC中,∠ABC=90°,AB=BC,AD∥BC,E是AB的中点,BE=AD. 13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是
13、如图,△DEF是由△ABC平移得到的,若BC=6cm,E是BC的中点,则平移的距离是 方作等边△CDE,连接BE.
方作等边△CDE,连接BE. 如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的
如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的