题目内容
已知线段AC=8,BD=6.
(1)已知线段AC垂直于线段BD.设图(1)、图(2)和图(3)中的四边形ABCD的面积分别为S1,S2和S3,则S1=
(2)如图(4),对于线段AC与线段BD垂直相交(垂足O不与点A,C,B,D重合)的任意情形,请你就四边形ABCD面积的大小提出猜想,并证明你的猜想.
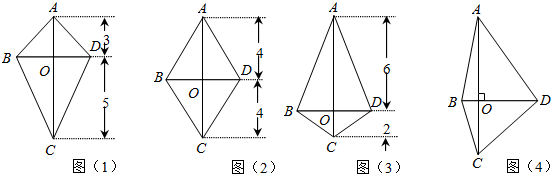
(1)已知线段AC垂直于线段BD.设图(1)、图(2)和图(3)中的四边形ABCD的面积分别为S1,S2和S3,则S1=
24
24
,S2=24
24
,S3=24
24
;(2)如图(4),对于线段AC与线段BD垂直相交(垂足O不与点A,C,B,D重合)的任意情形,请你就四边形ABCD面积的大小提出猜想,并证明你的猜想.

分析:(1)把四边形ABCD的面积分成△ABD和△BCD的和,然后列式求解即可;
(2)猜想,四边形的面积等于互相垂直的对角线乘积的一半,然后根据四边形ABCD的面积分成△ABD和△BCD的和进行证明.
(2)猜想,四边形的面积等于互相垂直的对角线乘积的一半,然后根据四边形ABCD的面积分成△ABD和△BCD的和进行证明.
解答:解:(1)S1=
×6×3+
×6×5=9+15=24,
S2=
×6×4+
×6×4=12+12=24,
S3=
×6×6+
×6×2=18+6=24;
(2)猜想四边形ABCD面积为24,
理由如下:S四边形ABCD=S△ABD+S△BCD,
=
BD•AO+
BD•CO,
=
BD(AO+CO),
=
BD•AC,
=
×8×6,
=24.
| 1 |
| 2 |
| 1 |
| 2 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
S3=
| 1 |
| 2 |
| 1 |
| 2 |
(2)猜想四边形ABCD面积为24,
理由如下:S四边形ABCD=S△ABD+S△BCD,
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=24.
点评:本题考查了多边形,三角形的面积,把四边形的面积分成两个三角形的面积的和是解题的关键,利用规则图形的面积求不规则图形的面积是常用的方法之一.

练习册系列答案
相关题目
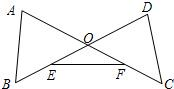 14、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.(1)添加条件∠A=∠D,OE=OF,试说明:AB=DC;
14、已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF.(1)添加条件∠A=∠D,OE=OF,试说明:AB=DC; 已知线段AC=8cm,点B是线段AC的中点,点D是线段BC的中点,求线段AD的长.
已知线段AC=8cm,点B是线段AC的中点,点D是线段BC的中点,求线段AD的长.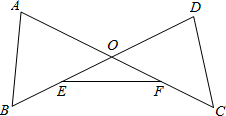 已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).
已知线段AC与BD相交于点O,连接AB、DC,E为OB的中点,F为OC的中点,连接EF(如图所示).