题目内容
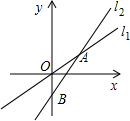如图，已知两直线l1和l2相交于点A（4，3），且OA=OB，请分别求出两条直线对应的函数解析式．
解：设L1为y=k1x，
4k1=3，k1=
，即L1为：y=x
∵A（4，3）
∴OA=5=OB
∴B（0，-5）
设L2为y=k2x+b．则有：
，
∴k2=2，
即L2为：y=2x-5．
分析：先用待定系数法求出设L1的解析式，再根据OA=OB可求出B的坐标，把A，B两点代入直线l2的解析式及可．
点评：本题要注意利用一次函数的特点，列出方程，求出未知数，再根据一次函数图象的特点解答，需同学们熟练掌握．
4k1=3，k1=
，即L1为：y=x∵A（4，3）
∴OA=5=OB
∴B（0，-5）
设L2为y=k2x+b．则有：
，∴k2=2，
即L2为：y=2x-5．
分析：先用待定系数法求出设L1的解析式，再根据OA=OB可求出B的坐标，把A，B两点代入直线l2的解析式及可．
点评：本题要注意利用一次函数的特点，列出方程，求出未知数，再根据一次函数图象的特点解答，需同学们熟练掌握．
练习册系列答案
相关题目
如图，已知两直线l1和l2相交于点A（4，3），且OA=OB，请分别求出两条直线对应的函数解析式．
已知两直线l1，l2分别经过点A（3，0），点B（-1，0），并且当两直线同时相交于y负半轴的点C时，恰好有l1⊥l2，经过点A、B、C的抛物线的对称轴与直线l2交于点D，如图所示．
