Question

【题目】如图1，正方形中，点、的坐标分别为，，点在第一象限．动点在正方形的边上，从点出发沿匀速运动，同时动点以相同速度在轴上运动，当点运动到点时，两点同时停止运动，设运动时间为秒．当点在边上运动时，点的横坐标(单位长度)关于运动时间(秒)的函数图象如图2所示．

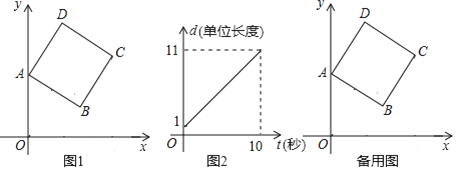
（1）正方形边长_____________，正方形顶点的坐标为__________________；

（2）点开始运动时的坐标为__________，点的运动速度为_________单位长度/秒；

（3）当点运动时，点到轴的距离为，求与的函数关系式；

（4）当点运动时，过点分别作轴，轴，垂足分别为点、，且点位于点下方，与能否相似，若能，请直接写出所有符合条件的的值；若不能，请说明理由．

Answer 1

【答案】（1）10，（14.12）；（2）（1，0），1；（3）d＝ t﹣4；（4）t的值为6s或 s或 s．

【解析】

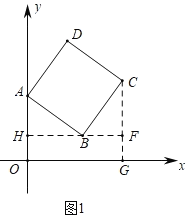
（1）过点B作BH⊥y轴于点H，CF⊥HB交HB的延长线于点F交x轴于G．利用全等三角形的性质解决问题即可．

（2）根据题意，易得Q（1，0），结合P、Q得运动方向、轨迹，分析可得答案；

（3）分两种情形：①如图3﹣1中，当0＜t≤10时，作PN⊥x轴于N，交HF于K．②如图3﹣2中，当10＜t≤20时，作PN⊥x轴于N，交HF于K．分别求解即可解决问题．

（4）①如图4﹣1中，当点P在线段AB上时，有两种情形．②如图4﹣2中，当点P在线段BC上时，只有满足时，△APM∽△PON，利用（3）中结论构建方程即可解决问题．

解：（1）过点B作BH⊥y轴于点H，CF⊥HB交HB的延长线于点F交x轴于G．

∵∠ABC＝90°＝∠AHB＝∠BFC

∴∠ABH+∠CBF＝90°，∠ABH+∠BAH＝90°，

∴∠BAH＝∠CBF，∵AB＝BC，

∴△ABH≌△BCF．

∴BH＝CF＝8，AH＝BF＝6．

∴AB＝＝10，HF＝14，

∴OG＝FH＝14，CG＝8+4＝12．

∴所求C点的坐标为（14，12）．

故答案为10，（14，12）

（2）根据题意，易得Q（1，0），

点P运动速度每秒钟1个单位长度．

故答案为（1，0），1．

（3）①如图3﹣1中，当0＜t≤10时，作PN⊥x轴于N，交HF于K．

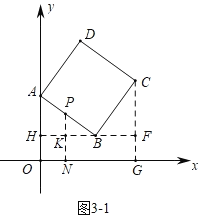
易知四边形OHKN是矩形，可得OH＝KN＝4，

∵PK∥AH，

∴，

∴，

∴PK＝（10﹣t），

∴d＝PK+KN＝﹣t+10．

②如图3﹣2中，当10＜t≤20时，作PN⊥x轴于N，交HF于K．

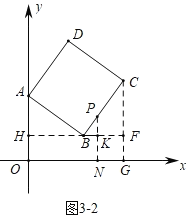
同法可得PK＝（t﹣10），

∴d＝PK+KN＝t﹣4．

（4）①如图4﹣1中，当点P在线段AB上时，有两种情形：

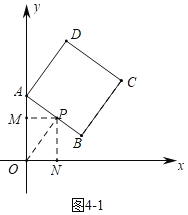
当时，△APM与△OPN相似，可得，

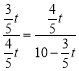解得t＝6．

当时，△APM与△OPN相似，可得，

解得t＝．

②如图4﹣2中，当点P在线段BC上时，只有满足时，△APM∽△PON，

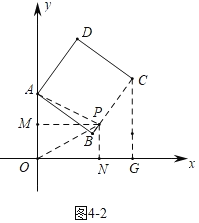
可得：∠OPN＝∠PAM＝∠AOP，

∵PM⊥OA，

∴AM＝OM＝PN＝5，

由（3）②可知：5＝t﹣4，

解得t＝．

综上所述，拇指条件的t的值为6s或s或s．