题目内容
3. 如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )
如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 135° |
分析 先根据射线OD平分∠AOC,∠AOD=∠COD,射线OE平分∠BOC,得∠COE=∠BOE,再根据∠AOC+∠BOC=180°,得出∠DOE=90°,由射线OF平分∠DOE,得∠DOF=∠EOF=45°,从而求得∠FOB+∠DOC的度数.
解答 解:∵射线OD平分∠AOC,
∴∠AOD=∠COD,
∵射线OE平分∠BOC,
∴∠COE=∠BOE,
∵∠AOC+∠BOC=180°,
∴∠DOE=∠DOC+∠EOC=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=90°,
∵OF平分∠DOE,
∴∠DOF=∠EOF=$\frac{1}{2}$∠DOE=45°,
∴∠FOB+∠DOC=∠BOF+∠AOD=180°-∠DOF=180°-45°=135°.
故选:D.
点评 本题考查了角的计算和角平分线的定义,一定要注意角平分线的几种表示方法.如:∠1=∠2,∠1=$\frac{1}{2}$∠AOB,∠AOB=2∠1.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
11. 如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
 如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
18.化简$\frac{\sqrt{-{a}^{3}}}{-a}$的结果是( )
| A. | $\sqrt{a}$ | B. | $\sqrt{-a}$ | C. | -$\sqrt{a}$ | D. | -$\sqrt{-a}$ |
15.某中学举行校园歌手大赛,7位评委给选手小明的评分如下表:
若比赛的计分方法是:去掉一个最高分,去掉一个最低分,其余分数的平均值作为该选手的最后得分,则小明的最后得分为( )
| 评委 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 得分 | 9.8 | 9.5 | 9.7 | 9.8 | 9.4 | 9.5 | 9.4 |
| A. | 9.56 | B. | 9.57 | C. | 9.58 | D. | 9.59 |
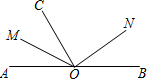 如图,O是直线AB上一点,OM平分∠AOC、ON平分∠BOC.
如图,O是直线AB上一点,OM平分∠AOC、ON平分∠BOC. 如图,在Rt△ABC中,∠ACB=90°,点O是AB上的动点,⊙O过点B交AB于点D,OE⊥AC,垂足为E,DE的延长线交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,点O是AB上的动点,⊙O过点B交AB于点D,OE⊥AC,垂足为E,DE的延长线交BC的延长线于点F.